
全程设计 第二章 平面解析几何 2.6 双曲线及其方程 2.6.2 双曲线的几何性质
第二章 平面解析几何 2.6 双曲线及其方程 2.6.2 双曲线的几何性质
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航、 课标定位素养阐释 L.了解双曲线的几何性质 2.掌握双曲线的渐近线和离心率的求解 3.能够灵活地解答一些与几何性质有关的双曲线问题 4.加强直观想象和数学运算能力的培养
导航 课标定位素养阐释 1.了解双曲线的几何性质. 2.掌握双曲线的渐近线和离心率的求解. 3.能够灵活地解答一些与几何性质有关的双曲线问题. 4.加强直观想象和数学运算能力的培养

导航 课前·基础认知 双曲线的几何性质 【问题思考】 L根据曲线F的方程器-总1(,6>,你能得到曲线F有哪 些性质? 提示:(1)≤M或x之M,y∈R;(2)曲线F关于x轴、y轴、原点对 称;3)曲线F与x轴交于点(士,0)等
导航 课前·基础认知 双曲线的几何性质 【问题思考】 1.根据曲线F的方程 (a>0,b>0),你能得到曲线F有哪 些性质? 提示:(1)x≤-a或x≥a,y∈R;(2)曲线F关于x轴、y轴、原点对 称;(3)曲线F与x轴交于点(±a,0)等. 𝒙 𝟐 𝒂𝟐 − 𝒚 𝟐 𝒃 𝟐 =1
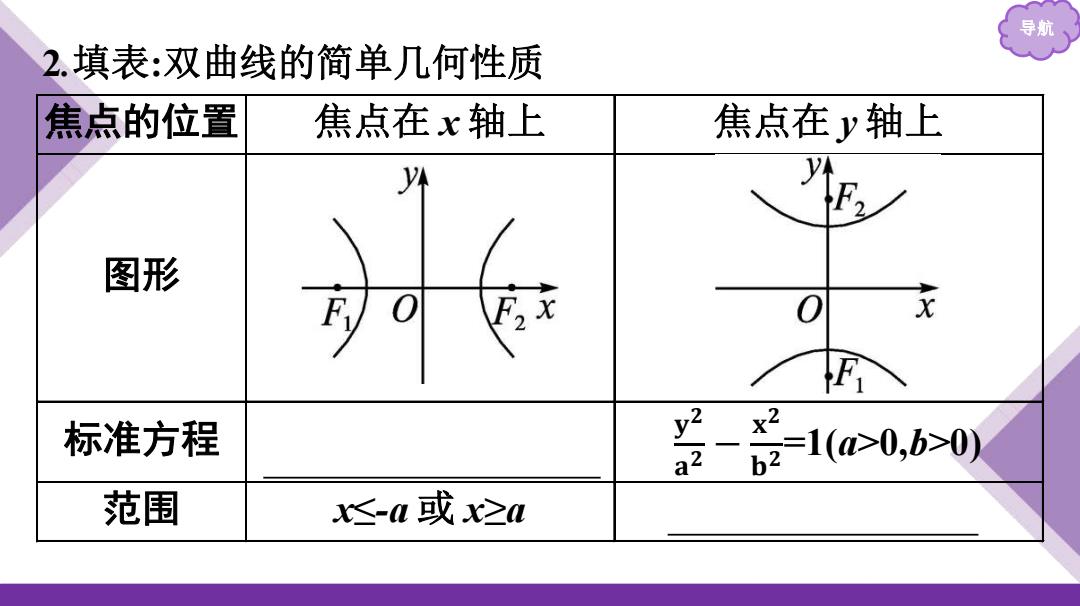
导航 2.填表:双曲线的简单几何性质 焦点的位置 焦点在x轴上 焦点在y轴上 图形 寸可 标准方程 至-器l0e,a0y 范围 ≤-n或之a
导航 2 .填表 :双曲线的简单几何性 质 焦点的位置 焦点在 x 轴上 焦点在 y 轴上 图形 标准方程 𝐱 𝟐 𝐚 𝟐 − 𝐲 𝟐 𝐛 𝟐 =1(a>0,b>0) 𝐲 𝟐 𝐚 𝟐 − 𝐱 𝟐 𝐛 𝟐 =1(a>0,b>0) 范围 x≤-a 或 x≥ a y ≤-a 或 y ≥ a