
第五节函数的微分 例1求函数y=x2在x=1和x=3处的微分. 解 例2求函数y=Vx当x0=4,△x=0.03时的增量和 微分 解 在例2中,△y=0.007486,dy=0.0075,所以△y≈dy. 一般地,若y=f)在x处可微,且|△x|很小,则 △y=dy+o(dy)△y≈dy. 上页 下页 返回 MathGS 公式 线与面 数学家
第五节 函数的微分 例1 求函数 y = x 2 在 x = 1 和 x = 3 处的微分. 第五节 函数的微分 解 例1 求函数 y = x 2 在 x = 1 和 x = 3 处的微分. 由微分的定义 dy = f (x0 )x 有 y f x d | x=1 = (1) = 2x , y f x d | x=3 = (3) = 6x . 例2 求函数 第五节 函数的微分 解 例2 求函数 y = x 当 x0 = 4 , x = 0.03 时的增量和 微分. 0 0 y = x + x − x = 4.03 − 4 = 2.007486 − 2 = 0.007486 , dy = f (x )x 0 x x = 2 0 1 4 0.03 = = 0.0075 . 在工具箱的函数求 值器中计算 y = x 当 x0 = 4 , x = 0.03 时的增量和 微分. 在例2中,y = 0.007486,dy = 0.0075,所以y dy . 一般地,若 y = f (x) 在 x0 处可微,且 | x | 很小,则 y = dy + o(dy) y dy
第五节函数的微分 二、微分的几何意义 如图所示,设Mx,yo),Nc+△x,Jyo+△y)为曲线 y=f()上的两点,且函数 y=f(x) y=fc)在x处可微,则曲 线在M处有切线,设为MT, △X 于是有 MQ=△x,QN=△y. ,+△ QP=MQ.tan=△x·f'(x),即dy=QP 上页 下页 返回 MathGS 公式 线与面 数学家
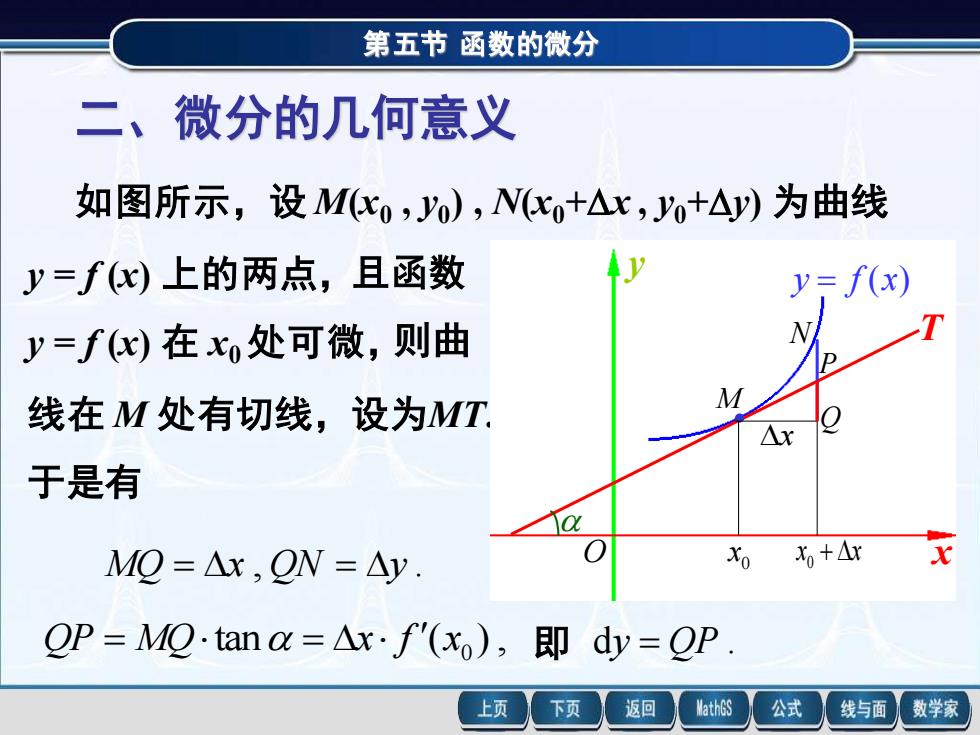
第五节 函数的微分 二、微分的几何意义 如图所示,设 M(x0 , y0 ) , N(x0+x , y0+y) 为曲线 y = f (x) 上的两点,且函数 y = f (x) 在 x0 处可微,则曲 线在 M 处有切线,设为MT. 于是有 MQ = x , QN = y . tan ( ) , 0 QP = MQ = x f x 即 dy = QP . M N Q P 0 x x + x 0 x x y T y = f (x) O