
在实际应用中,往往根据问题的实际意义去判断两事件是 否独立. 例如 甲、乙两人向同一目标射击,记A={甲命中}, B={乙命中},A与B是否独立? 由于“甲命中”并不影响“乙命中”的概率,故认为A、B 独立. 说明:两个事件相互独立,是指其中一个事件的发生,不影 响另一个发生的概率
在实际应用中,往往根据问题的实际意义去判断两事件是 否独立. 例如 由于“甲命中”并不影响“乙命中”的概率,故认为A 、 B 独立 . 甲、乙两人向同一目标射击,记 A ={甲命中}, B ={乙命中}, A与B是否独立? 说明:两个事件相互独立,是指其中一个事件 的发生,不影 响另一个发生的概率

又如:一批产品共n件,从中抽取2件, 设A,={第i件是合格品}i=1,2 若抽取是有放回的, 则A1与A2独立. 因为第二次抽取的结果不受第一次抽取的影响, 若抽取是无放回的,则A1与A2不独立 因为第二次抽取的结果受到第一次抽取的影响
一批产品共 件,从中抽取2件, 设 ={第 件是合格品} i=1,2 若抽取是有放回的, 则A 1与A 2独立. 因为第二次抽取的结果受到第一次抽取的影响. 又如: 因为第二次抽取的结果不受第一次抽取的影响. 若抽取是无放回的,则A 1与A 2不独立. Ai n i
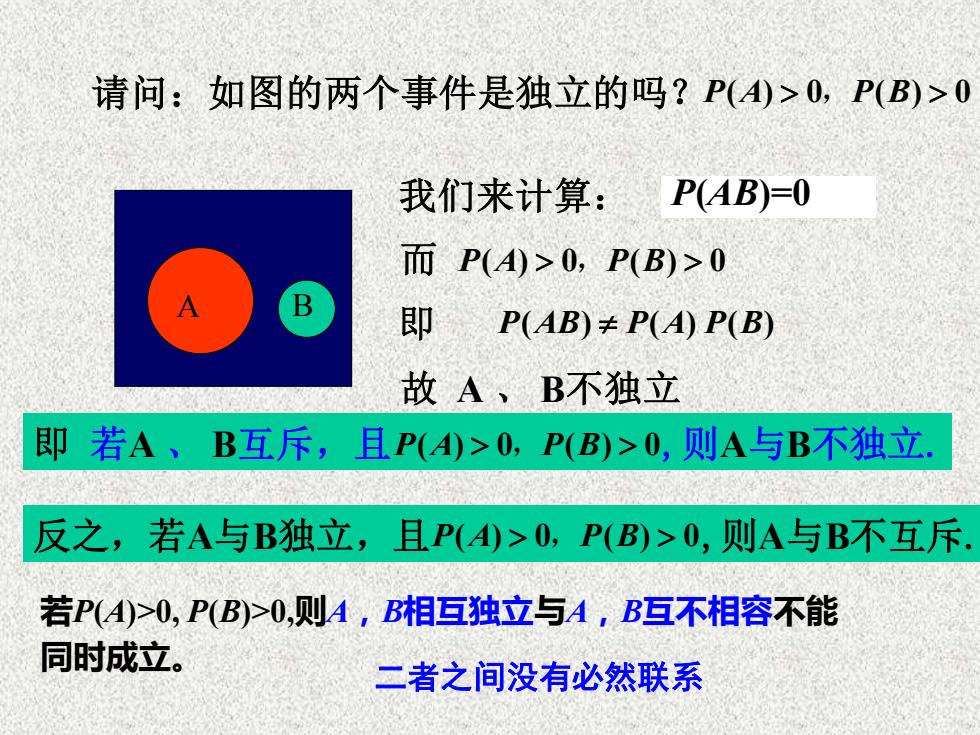
请问:如图的两个事件是独立的吗?P(A)>0,P(B)>0 我们来计算:P(AB)=0 而P(A)>0,P(B)>0 即 P(AB)≠P(AP(B) 故A、B不独立 即若A、B互斥,且P(A)>0,P(B)>0,则A与B不独立. 反之,若A与B独立,且P()>0,P(B)>0,则A与B不互斥, 若P(A)>0,P(B)>0,则A,B相互独立与A,B互不相容不能 同时成立。 二者之间没有必然联系
请问:如图的两个事件是独立的吗? A B 即 若A 、 B互斥,且 ,则A与B不独立. 反之,若A与B独立,且 ,则A与B不互斥. 而 故 A 、 B不独立 我们来计算: P(AB)=0 即 P A P B ( ) 0 ( ) 0 , P AB P A P B ( ) ( ) ( ) P A P B ( ) 0 ( ) 0 , P A P B ( ) 0 ( ) 0 , P A P B ( ) 0 ( ) 0 , 若P(A)>0, P(B)>0,则A,B相互独立与A,B互不相容不能 同时成立。 二者之间没有必然联系

前面我们看到独立与互斥的区别和联系, 再请你做个小练习. 设A,B为互斥事件,且P(4)>0,P(B)>0,下面四 个结论中,正确的是: 1.P(BA)>0 2.P(A|B)=P(A) 3.P4B)=0/4.PAB)=P4AP(B) 设A、B为独立事件,且P(4)>0,P(B)>0,下面四 个结论中,正确的是: 1.PBA)>02.P4B)=P(4) 3.PAB)=0 4.P(AB)=P(A)P(B) JJ
设A、B为互斥事件,且P(A)>0,P(B)>0,下面四 个结论中,正确的是: 前面我们看到独立与互斥的区别和联系, 1. P(B|A)>0 2. P(A|B)=P(A) 3. P(A|B)=0 4. P(AB)=P(A)P(B) 设A、B为独立事件,且P(A)>0,P(B)>0,下面四 个结论中,正确的是: 1. P(B|A)>0 2. P(A|B)=P(A) 3. P(A|B)=0 4. P(AB)=P(A)P(B) 再请你做个小练习

二、多个随机事件相互独立 1.三事件相互独立的概念 定义2:三事件相互独立 设A,B,C是三个事件,如果满足等式 P(AB)=P(A)P(B), P(BC)=P(B)P(C),→事件A,B,C两两相互独立. P(AC)=P(A)P(C), P(ABC)=P(A)P(B)P(C), 则称事件A,B,C相互独立· 注意三个事件相互独立一三个事件两两独立
注意 三个事件相互独立 三个事件两两独立. 定义2:三事件相互独立 设 A B C , , , 是三个事件 如果满足等式 A B C , , . 事件 两两相互独立 ( ) ( ) ( ), ( ) ( ) ( ), ( ) ( ) ( ), ( ) ( ) ( ) ( ), P AB P A P B P BC P B P C P AC P A P C P ABC P A P B P C = = = = 则称事件 A B C , , . 相互独立 二、多个随机事件相互独立 1. 三事件相互独立的概念