
例2求抛物线y2=2x与直线x-y=4所围成的图 形的面积 解题步骤: (1)画出函数的图形,并求出交点。 (2)求出微元素 (3)把微元素累加起来,取极限得图形的面积一一 定积分。 2009年7月3日星期五 6 目录○ 上页下页 返回
2009年7月3日星期五 6 目录 上页 下页 返回 例 2 求抛物线 2 y x = 2 与直线 x y − = 4 所围成的图 形的面积. 解题步骤: ( 1 )画出函数的图形, 并求出交点。 ( 2 )求出微元素 ( 3 )把微元素累加起来,取极限得图形的面积—— 定积分

例3求椭圆 户1所围图形的面积 解:利用对称性,有dA=ydx 4-4ydx 利用椭圆的参数方程 ox x+dxa x x=acost y=bsint (0≤t≤2π) 应用定积分换元法得 bsin(asin)b sin2d =4ah~2号=ab 当a=b时得圆面积公式 2009年7月3日星期五 7 目录 上页 下页 返回
2009年7月3日星期五 7 目录 上页 下页 返回 a b o x y x 1 2 2 2 2 =+ b y a x 解 : 利用对称性 , A = y dd x 所围图形的面积 . 有 ∫ = a xyA 0 d4 利用椭圆的参数方程 )20( sin cos ≤≤ π ⎩ ⎨ ⎧ = = t tby ax t 应用定积分换元法得 ∫ = 0 2 4 π A bsin t ⋅ − a t d)sin( t ∫ = 2 0 2 dsin4 π ttba = 4 ba 2 1⋅ 2 π ⋅ = π ba 当 a = b 时得圆面积公式 x + d x 例3 求椭圆

设p(0)∈C[C,B],p(0)≥0,求由曲线r=p(0)及 射线B=α,0=B围成的曲边扇形的面积 在区间[a,B]上任取小区间[0,0+d0] 则对应该小区间上曲边扇形面积的近似值为 d-jlod0 (θ 所求曲边扇形的面积为 A-ON X 2009年7月3日星期五 8 目录 上页 下页 返回
2009年7月3日星期五 8 目录 上页 下页 返回 设 ϕ θ ∈ C α β ϕ θ ≥ ,0)(,],[)( 求由曲线 r = ϕ θ )( 及 射线 θ = α ,θ = β 围成的曲边扇形的面积 . r = ϕ θ )( α x θ d θ 在区间 α β ],[ 上任取小区间 θ ,[ θ + d θ ] 则对应该小区间上曲边扇形面积的近似值为 [ ] d)( θθϕ 2 1 d 2 A = 所求曲边扇形的面积为 θθϕ β α d)( 2 1 2 ∫ A = β
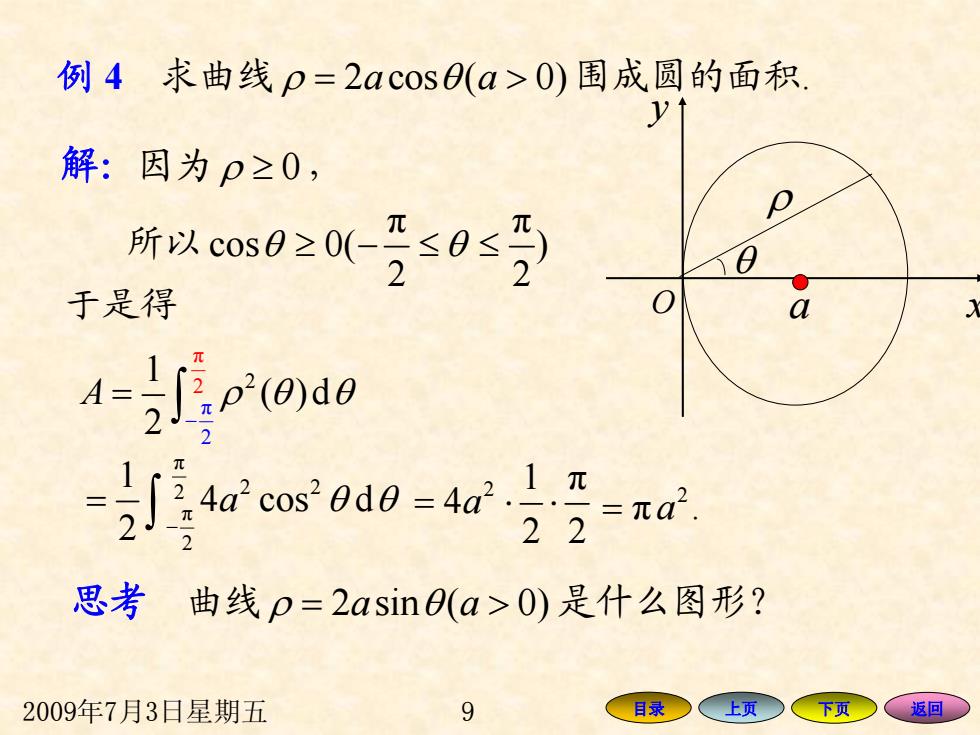
例4求曲线p=2acos0(a>0)围成圆的面积, 解:因为p≥0, 所以cms0≥0(-经s0s孕 于是 A-S.Od0 =星4acos0d0=4n.1a 22 =元a2 思考曲线p=2asin0(a>0)是什么图形? 2009年7月3日星期五 9 目录 上页 下页 返回
2009年7月3日星期五 9 目录 上页 下页 返回 例 4 求曲线 ρ = 2 cos ( 0) a a θ > 围成圆的面积. O x y a ρ θ 解:因为 ρ ≥ 0, 所以 π π cos 0( ) 2 2 θ θ ≥−≤≤ 于是得 π 2 π 1 2 2 ( )d 2 A ρ θ θ − = ∫ π 2 2 2 π 2 1 4 cos d 2 a θ θ − = ∫ 2 1 π 4 2 2 = a ⋅ ⋅ 2 = π a . 思考 曲线 ρ = 2 sin ( 0) a a θ > 是什么图形?