《线性代数》课程教学课件（PPT讲稿，A）§3.2 逆矩阵（§3.3 初等矩阵）

线性代数 第三章优花老三车三、可逆矩阵的性质结束四、典型例题

线性代数 第三章 三、可逆矩阵的性质 结束 四、典型例题

线性代数 第三章祥花光三草四、典型例题33121[21例2 A=202.2.B=C=15333求矩阵X使满足AXB = C.32解：2B=1±0,1=2±0,2三53334：A-1,B-1都存在

线性代数 第三章 1 2 3 1 3 2 1 2 , , , 2 2 1 2 0 5 3 3 4 3 3 1 . A B C X AXB C           = = =                 = 例 求矩阵 使满足 解: 2 0, 3 4 3 2 2 1 1 2 3  A = =  1 0, 5 3 2 1 B = =  , .  A −1 B −1都存在 四、典型例题 ∵

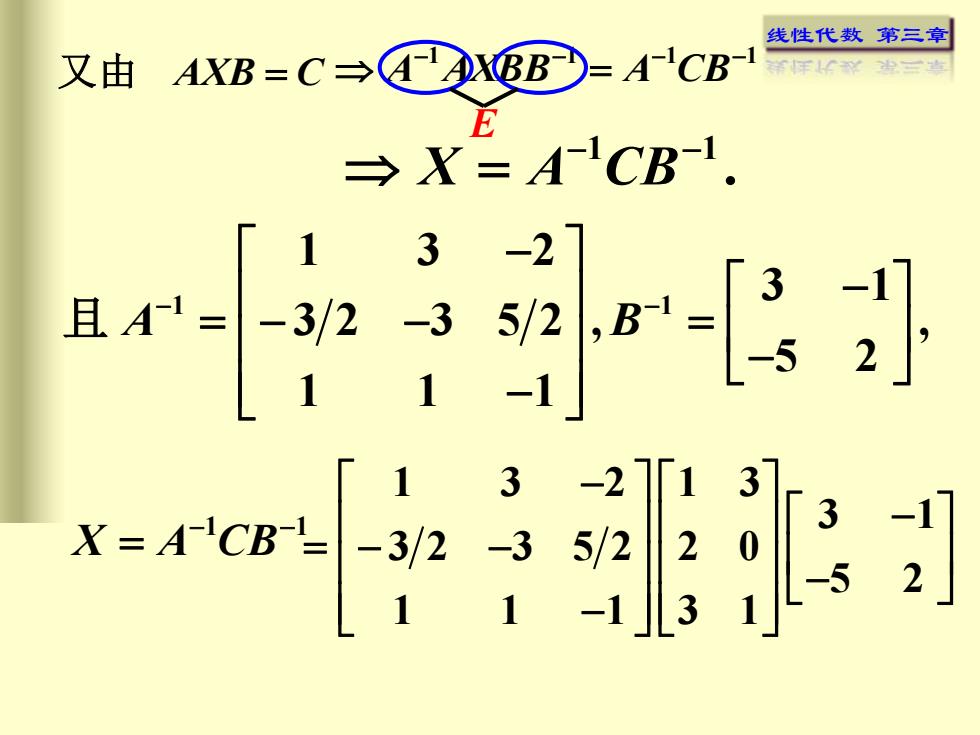
线性代数第三章)=A-'CB-又由A-AXBB-)祥样三堂AXB=C=E= X= A-1CB-13-2312 /,B-1 =且 A-1 =/-3/22-35/22-511-133-2113-1X = A-iCB-=|-3/2202-35/2523111-1

线性代数 第三章 又由 AXB = C −1 −1 −1 −1  A AXBB = A CB. −1 −1  X = A CB 1 3 2 1 3 3 1 3 2 3 5 2 2 0 5 2 1 1 1 3 1     −       − = − −         −         − E 1 1 1 3 2 3 1 3 2 3 5 2 , , 5 2 1 1 1 A B − −   −     − = = − −       −     − 且 −1 −1 X = A CB

线性代数第三章祥彩光三草33F1-23X = A-iCB-l=-3/2205/2-33-23-10-2102二2-502-104

线性代数 第三章 1 1 2 1 3 1 0 2 10 4 . 5 2 0 2 10 4     −       − = = − −         −         − 1 3 2 1 3 3 1 3 2 3 5 2 2 0 5 2 1 1 1 3 1     −       − = − −         −         − −1 −1 X = A CB

线性代数第三章祥样三堂3例3角(1)解矩阵方程X-32(2) X022

线性代数 第三章 ( ) ( ) 1 5 3 2 1 ; 1 4 1 4 1 1 1 1 2 3 2 ; 1 1 0 2 0 4 2 1 1 0 1 5 . X X     − =         −     − −     =             − 例 3 解矩 阵 方程