《线性代数》课程教学课件（PPT讲稿，A）§3.2 逆矩阵（§3.3 初等矩阵）

线性代数第三章Ai=j由于 aiA, +ai2Aj +...+ain祥花光三堂Ainij1Ai=jAaiAi +a2iAi +...+ann0itja1所以(n)2n2AA*-4a441nln22nnnInnnAE

线性代数 第三章 11 12 1 11 21 1 * 21 22 2 12 22 2 1 2 1 2 n n n n n n nn n n nn a a a A A A a a a A A A AA a a a A A A             =                           = A A A        0 0 0 0 0 0 由于 1 1 2 2 1 1 2 2 0 0 i j i j in jn i j i j ni nj A i j a A a A a A i j A i j a A a A a A i j  = + + + =     = + + + =    所以 = A E

线性代数 第三章祥花光三草同理可得：IA|0A=A|EA"A[AlAA* =A'A=|AE故只要A|±0，就有A(A)A=E

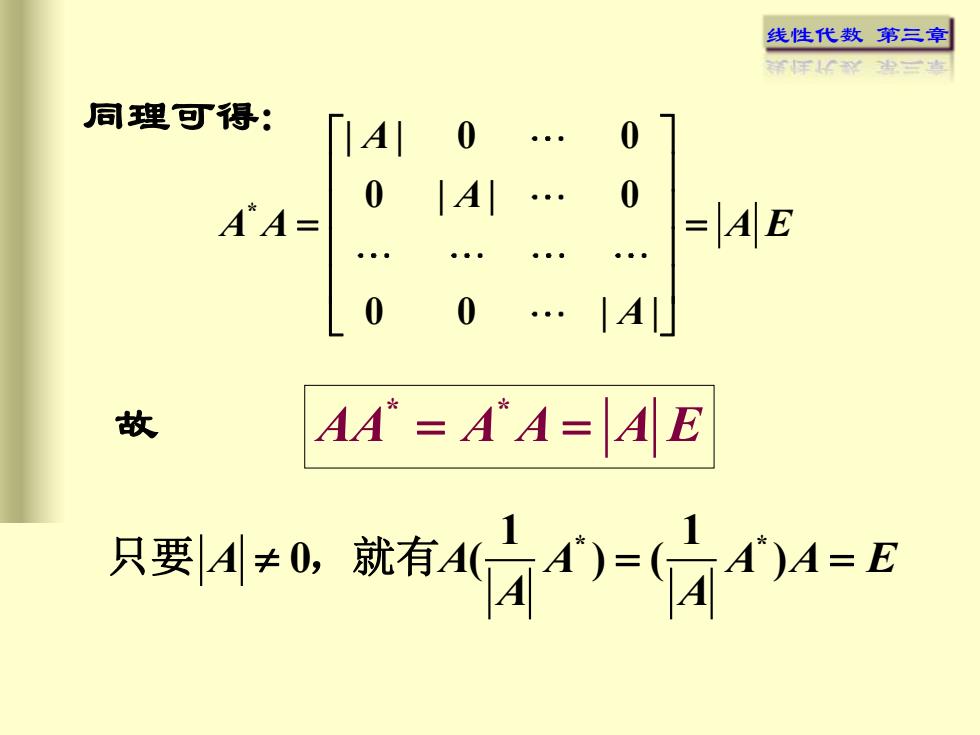
线性代数 第三章 同理可得: * | | 0 0 0 | | 0 0 0 | | A A A A A E A     = =         * * 故 AA A A A E = = 1 1 * * A A A A A E 0 ( ) ( ) A A 只要  = = ，就有

线性代数 第三章定理3.2.1（可逆的充分必要条件）第花老三n阶方阵A可逆A|0，而且A-1A证明：已证"←"(充分)"="(必要)若A可逆，则存在A-，使得AA-=E两边取行列式，得：IAA-=|AILA-EI=1IA± 0.所以

线性代数 第三章 定理3.2.1（可逆的充分必要条件） . | | 1 | | 0 − 1    = A A n 阶 方 阵 A 可 逆 A ，而且 A 证明： ""(充分) 已证. ""(必要) 1 1 A A AA E − − 若 可逆，则存在 ，使得 = 两边取行列式，得： 1 1 | | | || | | | 1 AA A A E − − = = = 所以 | A| 0

线性代数 第三章老三草V推论若A是n阶矩阵，且存在n阶矩阵B，使AB=E 或BA=E则A可逆，且B为A的逆矩阵判断B是否为A的逆矩阵只需验证AB=E和BA=E中的一个即可B= EB =(A-A)B= A-(AB)= A-"E = A-1同理可证，若 BA=E，则 B=A-1

线性代数 第三章 推论 若A是n阶矩阵，且存在n阶矩阵B，使 A B = E 或 B A = E 则A可逆，且B为A的逆矩阵. 证明：设AB=E 则 | | | || | | | 1 AB A B E = = = 所以 | | 0, A  由定理可知，A可逆. 设其逆矩阵为A -1 ,则有： B EB = = 1 ( ) A A B − 1 A AB ( ) − = 1 A E− = 同理可证，若 BA = E，则 1 B A . − = 1 A − = B A AB E BA E = = 判断 是否为 的逆矩阵， 只需验证 和 中的一个即可

线性代数第三章2-1祥样花老三堂例1 判断A =31是否可逆？若可逆，求其逆矩阵0-20-1解：IA| 0.故A可逆，又Au=-2， A21=4,，A31=1,A12=-2， A22=-3， A32=-3241-A13=l， A23=-2， A33=-5,-9199-21于是21A-6-3-3-313135-91-92-5-219

线性代数 第三章 1 2 1 1 3 1 0 . 1 0 2 A   −   =     − −   例 判 断 是 否 可 逆 ？ 若 可 逆 ， 求 其 逆 矩 阵 解： 故 A 可逆，又 A11=-2， A21=4， A31=1， A12=-2， A22=-3， A32=-3 A13=1， A23=-2 , A33=-5 ， 于是 1 * 2 4 1 1 1 6 3 3 9 1 2 5 A A A −   −   = = − −       − − 2 4 1 9 9 9 2 1 1 3 3 3 1 2 5 9 9 9   −      = − −       − −     | A| 0