《概率论与数理统计》课程教学资源（PPT课件）第1章 概率论的基本概念 第五节条件概率

概率伦与敖理统外 第五节 条件概率 一、条件概率 二、乘法定理 三、全概率公式与贝叶斯公式

一、条件概率 二、乘法定理 三、全概率公式与贝叶斯公式 第五节 条件概率

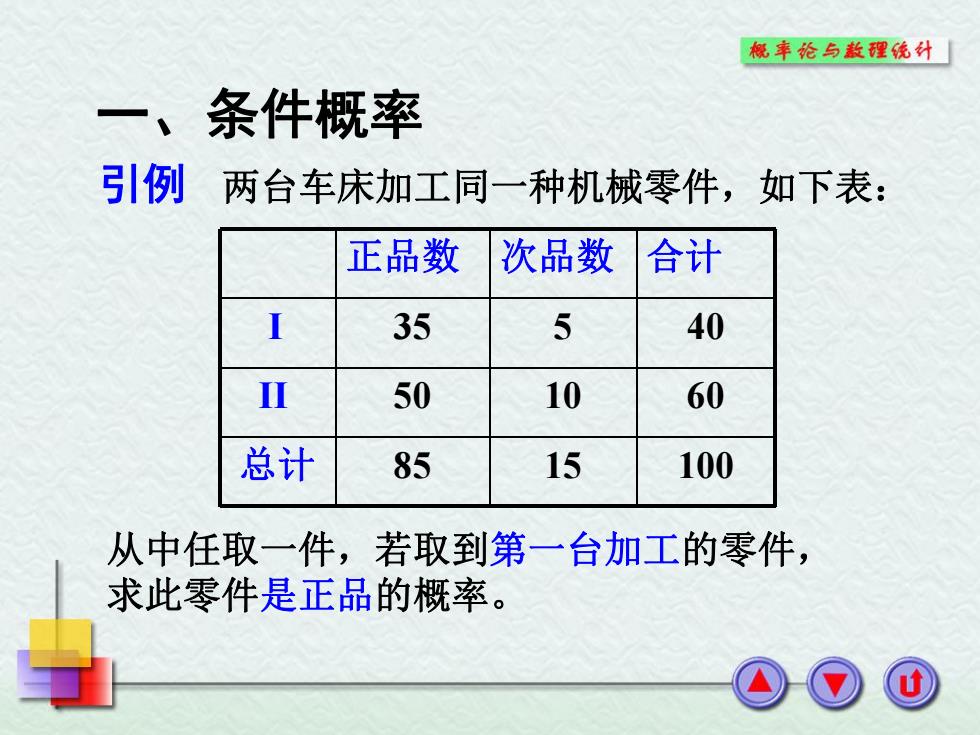
概奉论与散理统计「 一、条件概率 引例 两台车床加工同一种机械零件，如下表： 正品数 次品数 合计 35 5 40 Ⅲ 50 10 60 总计 85 15 100 从中任取一件，若取到第一台加工的零件， 求此零件是正品的概率

引例 两台车床加工同一种机械零件，如下表： 一 、条件概率 正品数 次品数 合计 I 35 5 40 II 50 10 60 总计 85 15 100 从中任取一件，若取到第一台加工的零件， 求此零件是正品的概率

概率论与款理统外 1.定义 设A,B是两个事件，且P(A)>0,称 P(BA)=P(AB) P(A) 为在事件A发生的条件下事件B发生的条件概率. 同理可得 P(AB)=P(AB) P(B) 为事件B发生的条件下事件A发生的条件概率

( ) ( ) ( ) P B P AB 同理可得 P AB  为事件 B 发生的条件下事件 A 发生的条件概率. . ( ) ( ) ( ) , , ( ) 0, 为在事件 发生的条件下事件 发生的条件概率 设 是两个事件 且 称 A B P A P AB P B A A B P A   1. 定义

概奉论与散理统计「 2.性质 (I)非负性：P(BA≥0； (2)规范性：P(SA)=1,P(OA)=0, (3)P(BUB A=P(B A+P(B A)-P(BB.A); (4)P(BA)=1-P(BA) (5)可列可加性：设B1,B2,.是两两不相容的事 件，则有 P084小-2P®

(3) ( ) ( ) ( ) ( ); P B1B2 A P B1 A P B2 A P B1B2 A (4) P(B A) 1 P(B A). (2) 规范性: P(S A) 1, P( A)  0; 件 则有 可列可加性 设 是两两不相容的事 , (5) : , , B1 B2  ( ). 1 1            i i i P Bi A P B A 2. 性质 (1)非负性: P(B A)  0;

概率论与数理统外 例1一个盒子中装有7件产品，包括4件一等品 和3件二等品，从中不放回地取三次，每次取一 件，令A1:第1次取到一等品，=1,2,3 P(A),P(A,A),P(A;A 42)

例1 一个盒子中装有7件产品，包括4件一等品 和3件二等品，从中不放回地取三次，每次取一 件，令 Ai: 第i次取到一等品，i=1,2,3 1 2 1 3 1 2 求 P( A ), P( A A ), P( A A A )