第二节定积分在几何上的应用 例3求椭圆 a2+b2 =1所围成的图形的面积, 解 3 b31 上页 下页 返回 MathGS 公式 线与面 数学家
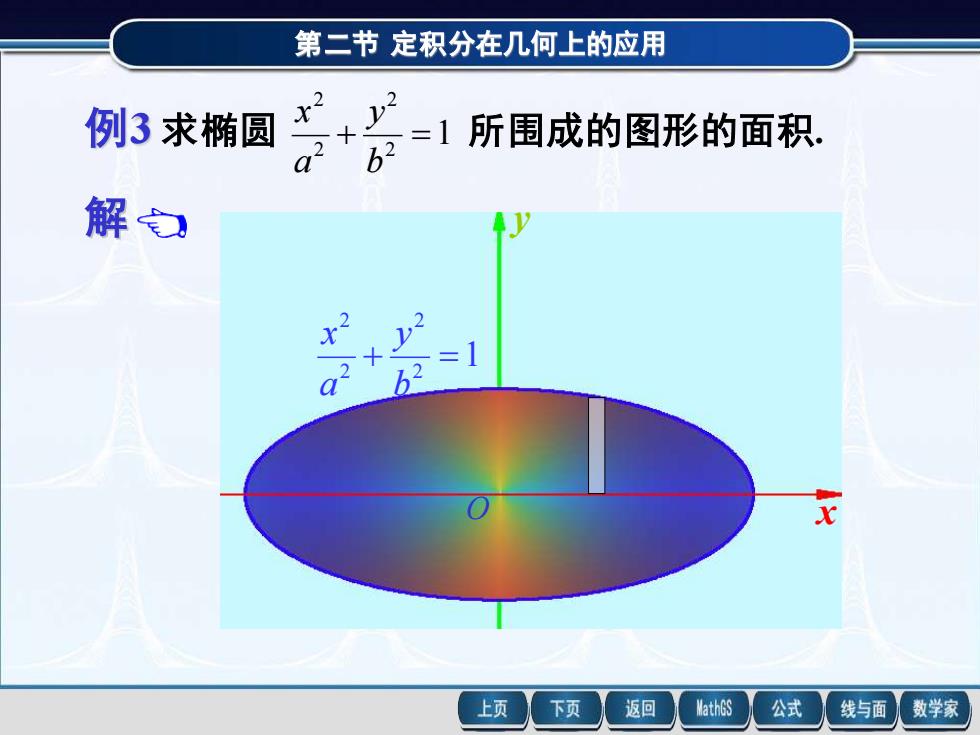
第二节 定积分在几何上的应用 例3 求椭圆 第二节 定积分在几何上的应用 x y O 1 2 2 2 2 + = b y a x 解 例3 求椭圆 1 所围成的图形的面积. 2 2 2 2 + = b y a x 选 x 为积分变量, 利用对称性,面积元素为 dA = ydx , 所求面积为 4 d . 0 = a A y x 利用椭圆的参数方程 = = 2 π 0 sin , cos , t y b t x a t 计算该定积分, 1 所围成的图形的面积. 2 2 2 2 + = b y a x x y O 1 2 2 2 2 + = b y a x
第二节定积分在几何上的应用 例4计算摆线 x=a(t-sin t), (a>0)的一拱与x轴所 y=a(1-cost), 围成的图形的面积。 解 y x=a(t-sin t) y=a(1-cost) 2元0X 摆线动画 上页 下页 返回 MathGS 公式 线与面 数学家
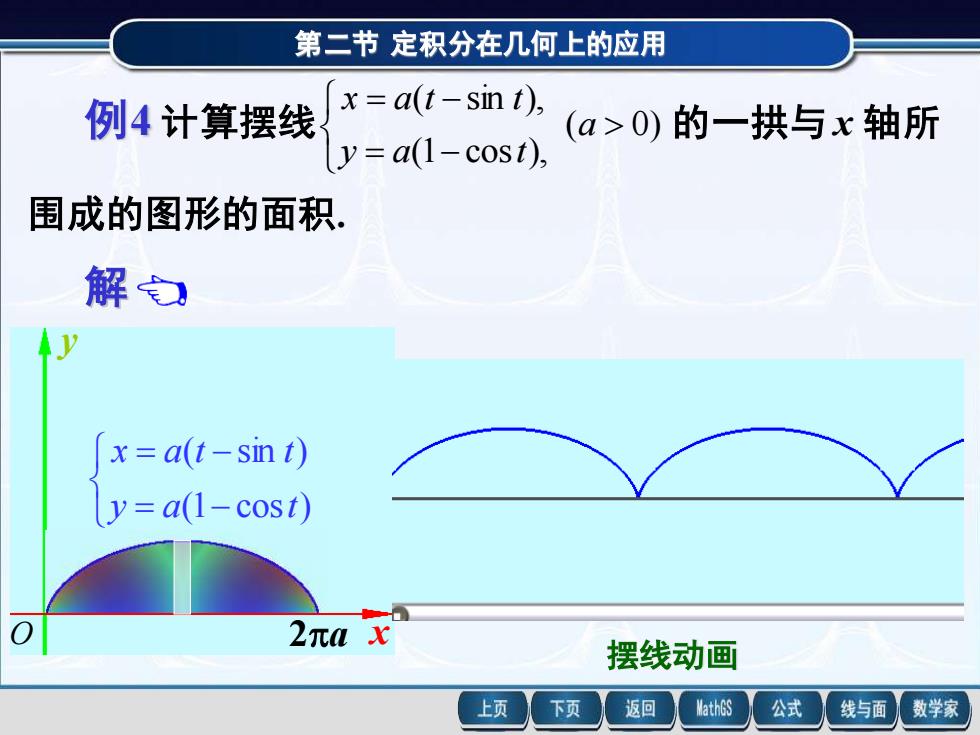
第二节 定积分在几何上的应用 x y O 2a = − = − (1 cos ) ( sin ) y a t x a t t 例4 计算摆线 第二节 定积分在几何上的应用 围成的图形的面积. 解 例4 计算摆线 ( 0) 的一拱与 x 轴所 (1 cos ), ( sin ), = − = − a y a t x a t t 所求面积为 = a A y x 2π 0 d = − − a a t a t t 2π 0 (1 cos )d[ ( sin )] = − 2π 0 2 2 a (1 cost) dt 3π . 2 = a x y O 2a = − = − (1 cos ) ( sin ) y a t x a t t ( 0) 的一拱与 x 轴所 (1 cos ), ( sin ), = − = − a y a t x a t t 围成的图形的面积. 摆线动画
第二节定积分在几何上的应用 例5计算星形线r+y=a(a>0)所围成的图形的 2 面积. 2 2 解 +y3 a3 星形线动画 上页 下页 返回 MathGS 公式 线与面 数学家
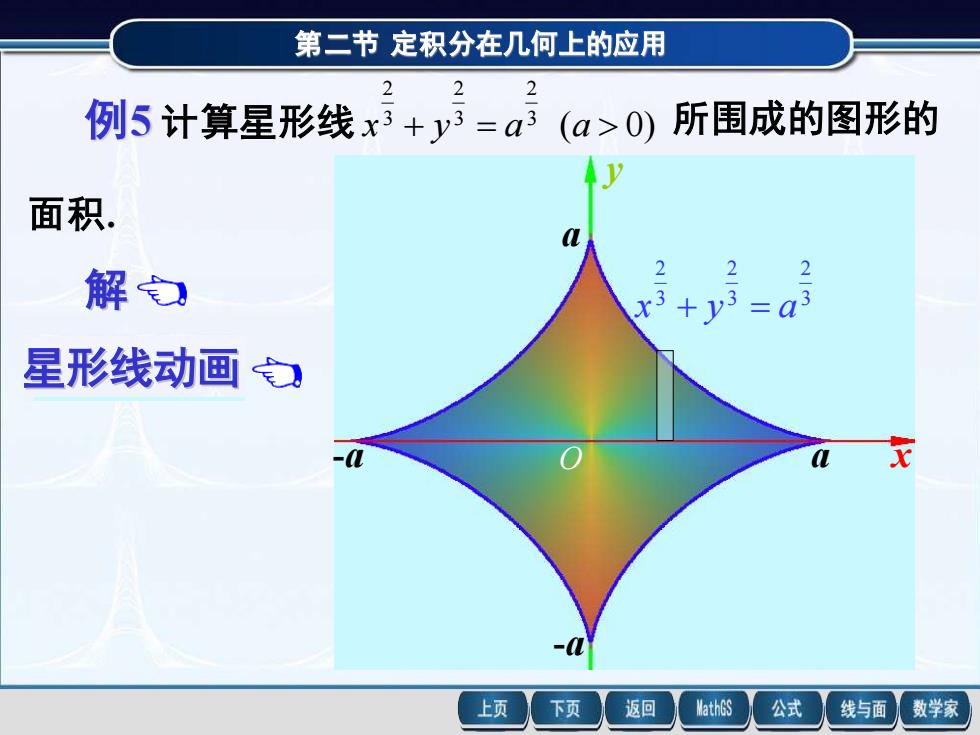
第二节 定积分在几何上的应用 例5 计算星形线 第二节 定积分在几何上的应用 3 2 3 2 3 2 x + y = a -a a -a a x y O 解 例5 计算星形线 3 ( 0) 所围成的图形的 2 3 2 3 2 x + y = a a 面积. 星形线的参数方程为 (0 2π). sin , cos , 3 3 = = t y a t x a t 由对称性可得 = a A y x 0 4 d = 0 2 π 3 3 4 asin td(a cos t) = 2 π 0 2 4 2 4a sin t cos tdt = − 2 π 0 2 4 6 4a (sin t sin t)dt π . 8 3 2 = a 3 ( 0) 所围成的图形的 2 3 2 3 2 x + y = a a 面积. 第二节 定积分在几何上的应用 星形线动画 星形线是内摆线的一种 3 2 3 2 3 2 x + y = a -a a -a a x y O

第二节定积分在几何上的应用 2.极坐标情形 设p(0)eCL,B],p(0)≥0,求由曲线p=p(0)及 射线0=a,0=B围成的曲边扇形的面积. 在区间[a,B]上任取小区间[0,0+d0],则对应小区 间上曲边扇形面积的近似值为 =p(0) dA-d0. do 所求曲边扇形的面积为 4-Jdo 上页 下页 返回 MathGS 公式 线与面 数学家
第二节 定积分在几何上的应用 2. 极坐标情形 求由曲线 = ( ) 及 射线 = , = 围成的曲边扇形的面积 . =() d 在区间[ , ]上任取小区间 间上曲边扇形面积的近似值为 ( ) d , 2 1 d 2 A = 所求曲边扇形的面积为 ( )d . 2 1 2 A = O x 设 ( )C[ , ] , ( ) 0 , 则对应小区
第二节定积分在几何上的应用 例6计算阿基米德螺线p=a0(a>0)上相应于0从 0变到2元的一段弧与极轴所围成的图形的面积. 解 2元0 p=0 上页 下页 返回 MathGS 公式 线与面 数学家
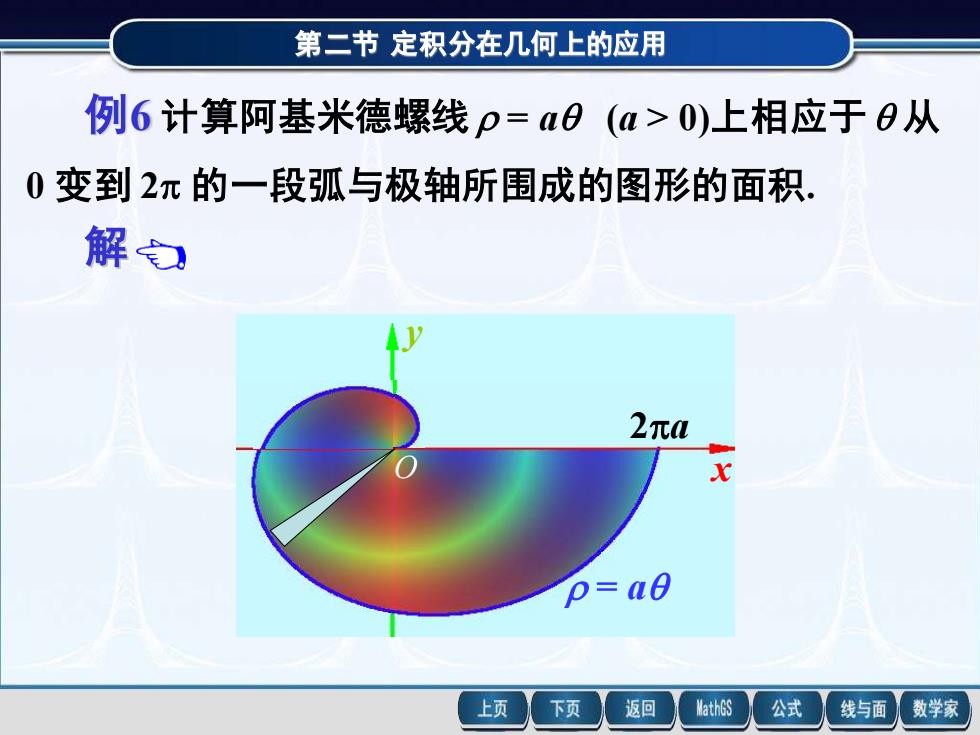
第二节 定积分在几何上的应用 例6 计算阿基米德螺线 = a (a > 0)上相应于 从 第二节 定积分在几何上的应用 解 例6 计算阿基米德螺线 = a (a > 0)上相应于 从 0 变到 2 的一段弧与极轴所围成的图形的面积. 由极坐标系下的面积公式,得 ( )d 2 1 2 A = ( ) d 2 1 2π 0 2 = a π . 3 4 2 3 = a = a 2a O x y 0 变到 2 的一段弧与极轴所围成的图形的面积. = a 2a O x y