
12 -1 0 1 2 -1 0 h40 -1 5 4 5-720 -1 J 4 = 0 -7 7 -1 r4-2n0 0 -28 -29 0 -2 3 3 00 -7 -5 12 -1 0 1 2 -1 0 0 -1 5 4 4-43 0 一1 5 4 =一 0 0 -7 -5 0 0 -7 -5 0 0 -28 -29 0 0 0 -9 =-1×(-1)×(-7)×(-9)=63. 由于化简过程具有程序化,因此工程技术上,常用计 算机编制程序计算高阶行列式的值
= −1(−1)(−7)(−9) = 63. 0 0 0 9 0 0 7 5 0 1 5 4 1 2 1 0 4 3 4 − − − − − = − r − r 0 0 28 29 0 0 7 5 0 1 5 4 1 2 1 0 3 4 − − − − − − = − r r 由于化简过程具有程序化,因此工程技术上,常用计 算机编制程序计算高阶行列式的值。 0 2 3 3 0 7 7 1 0 1 5 4 1 2 1 0 2 4 − − − − − = r r 0 0 7 5 0 0 28 29 0 1 5 4 1 2 1 0 3 2 4 2 7 2 − − − − − − = − − r r r r

例4设多项式 1、 2 3 2 3 f(x)= 2 3 5 2 3 试求f(x)=0的根. 解方法一 1 1 2 3 4-5 1 1 2 3 2 2-x2 2 U 3-24 01-x2 0 0 f(x)= 2 3 1 5 0 1 -3 -1 2 3 19-x2 2- 0 04-x2
− = − 2 2 1 1 2 3 1 2 2 3 ( ) . 2 3 1 5 2 3 1 9 x f x x 例4 设多项式 解 方法一 − = − 2 2 1 1 2 3 1 2 2 3 ( ) 2 3 1 5 2 3 1 9 x f x x 4 3 3 1 2 1 2 r r r r r r − − − − − − − 2 2 1 1 2 3 0 1 0 0 0 1 3 1 0 0 0 4 x x 试求 f x( ) 0 = 的根

2 3 11 2 3 分3 0 -3 -1 5-(1-x252 01 -3 -1 0 0 0 00 31-x2) 1-x 0 0 0 4-x2 00 0 4-x2 =-31-x2)(4-x2). 2 3 让f(x)=0,解得:x12=1,x3,4=+2. 1 2-x2 2 3 f(x) 2 3 9-x 方法二由性质1.2.2推论知,当2-x2=1或9-x2=5 时,方程成立,即x2=±1,x3,4=+2为f(x)=0的根 由于原方程为关于x的4次多项式,因此原方程只有4个根
2 3 r r − − − − − 2 2 1 1 2 3 0 1 3 1 0 1 0 0 0 0 0 4 x x 2 3 2 r x r − − (1 ) − − − − − − 2 2 2 1 1 2 3 0 1 3 1 0 0 3(1 ) 1 0 0 0 4 x x x = − − − 2 2 3(1 )(4 ). x x 让 f x( ) 0, = 解得:x x 1,2 3,4 = = 1, 2. 方法二 − = 2 由性质1.2.2推论知,当 2 1 x 或 − = 2 9 5 x 由于原方程为关于x的4次多项式,因此原方程只有4个根. 时,方程成立,即 x x 1,2 3,4 = = 1, 2 为 f x( ) 0 = 的根. 2 2 1 1 2 3 1 2 2 3 ( ) . 2 3 1 5 2 3 1 9 x f x x − = −
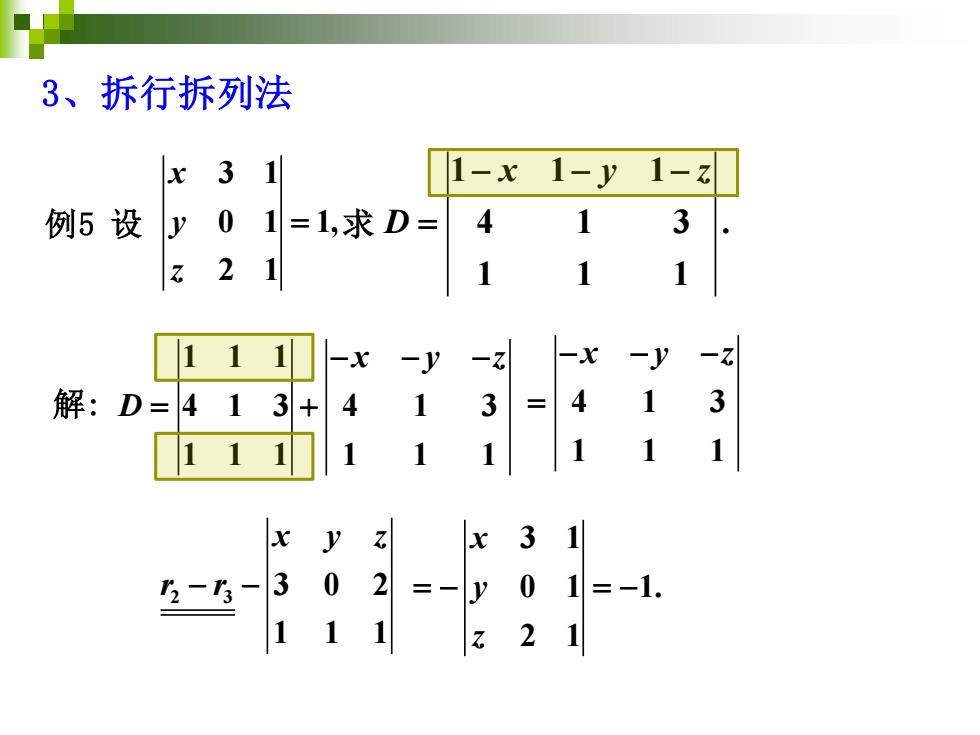
3、拆行拆列法 x31 1-x1-y 1-z 例5设 y01=1,求D= 4 3 z21 1 1 1 11 -x -v -z -x -y- 解: D= 4 13 4 1 3 1 3 1 1 1 1 1 11 1 31 2-3 3 0 2 y 01=-1. 11 1 z21
解: 3 1 0 1 1, 2 1 x y z 例5 设 = 求 1 1 1 4 1 3 . 1 1 1 x y z D − − − = 1 1 1 4 1 3 4 1 3 1 1 1 1 1 1 x y z D − − − = + 3、拆行拆列法 4 1 3 1 1 1 − − − x y z = 2 3 3 0 2 1 1 1 x y z r r − − 3 1 0 1 1. 2 1 x y z = − = −