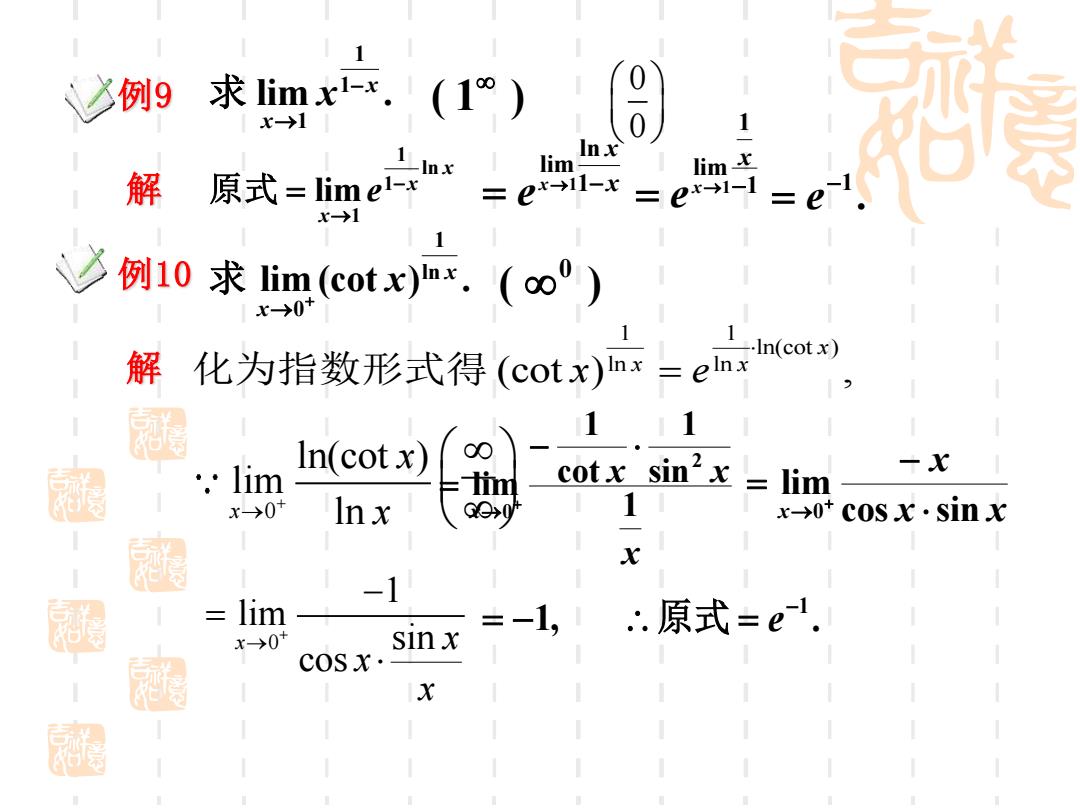
心9求四.(1)(8 1 x→1 1 Inx lim lim 解 原式=lime-x =ex-11-x =ex→1-1 x→1 例10求1 im (cotx).(o) x→0 解化为指数形式得(cotx)nx=elnx 1.In(cot x) 111 .lim In(cot x) cotx sin2x = 一X 威 lim x→0+ Inx G0→0 1 x→0tC0sx·SinX X -1 lim =-1,1.原式=e1. x-→0* sin x COSx· X
例9 解 lim . 1 1 1 x x x − → 求 ( 1 ) x x x e ln 1 1 1 lim − → 原式 = x x x e → − = 1 ln lim 1 1 1 lim →1− = x x e . −1 = e 例10 解 lim (cot ) . ln 1 0 x x x 求 → + ( ) 0 1 1 ln(cot ) ln ln (cot ) , x x x x e 化为指数形式得 = 0 ln(cot ) lim x ln x x → + x x x x 1 sin 1 cot 1 lim 2 0 − = → + x x x x cos sin lim 0 − = → + = −1, . −1 原式 = e 0 0 0 1 lim sin cos x x x x → + − =
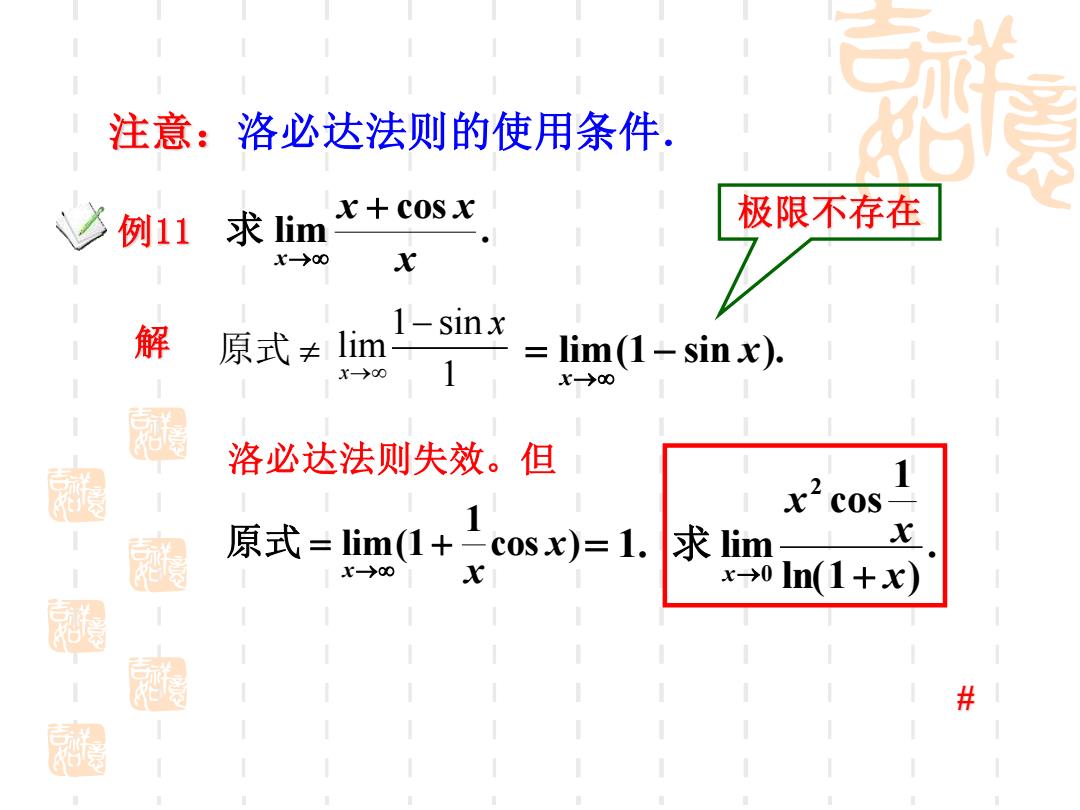
注意:洛必达法则的使用条件, 例11求im x+COSx 极限不存在 X→00 X 解 1-§ 原式≠m inx lim(1-sinx). X-→00 1 X→00 洛必达法则失效。但 x2cos 1 1 X 展 原式=lim(1+-cosx)=1.求im X→00 x x-→0ln(1+x) #
例11 解 . cos lim x x x x + → 求 1 sin lim x 1 x → − lim(1 sin x). x = − → 极限不存在 洛必达法则失效。但 cos ) 1 lim(1 x x x = + → 原式 = 1. 注意:洛必达法则的使用条件. . ln(1 ) 1 cos lim 2 0 x x x x→ + 求 # 原式
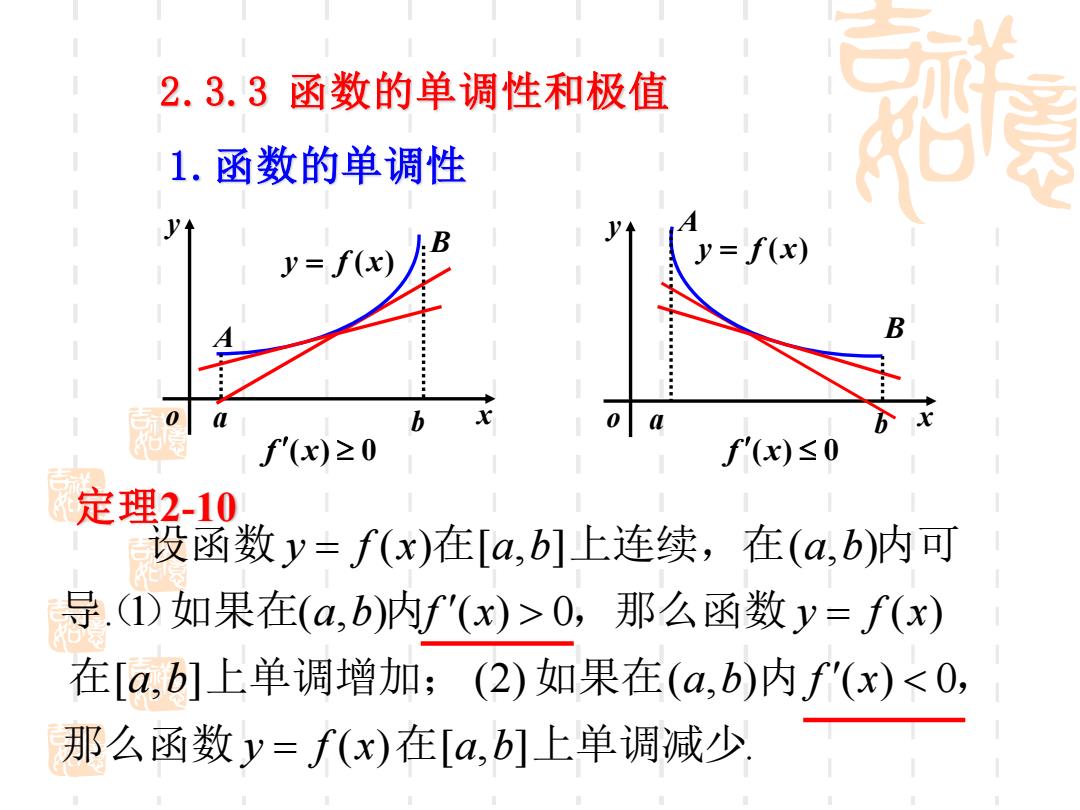
2.3.3函数的单调性和极值 1.函数的单调性 :f(x) =f(x) b f'(x)≥0 f'(x)≤0 定理2-10 设函数y=f(x)在[a,b]上连续,在(a,b)内可 导.(①)如果在(a,b)内f'(x)>0,那么函数y=f(x) 在[a,b]上单调增加;(2)如果在(a,b)内f'(x)<0, 那么函数y=f(x)在[a,b]上单调减少
1.函数的单调性 x y o y = f (x) x y o y = f (x) a b A B f (x) 0 f (x) 0 a b B A 2.3.3 函数的单调性和极值 定理2-10 ( ) [ , ] . [ , ] (2) ( , ) ( ) 0 . 1 ( , ) ( ) 0 ( ) ( ) [ , ] ( , ) 那么函数 在 上单调减少 在 上单调增加; 如果在 内 , 导()如果在 内 ,那么函数 设函数 在 上连续,在 内可 y f x a b a b a b f x a b f x y f x y f x a b a b = = =

证 Vx1,x2∈(M,b),且1<x2,应用拉氏定理,得 f(x2)-f()=f'(5)x2-x) (x1<5<x2) .x2-X1>0, 若在(a,b)内,f'(x)>0, 则'(5)>0, .f(2)>f()..y=f(x)在[,b上单调增加 若在(a,b)内,f'(x)<0,则f'(5)<0, .f(x2)<f(x)..y=f(x)在[a,b]上单调减少 如果函数在其定义域的某个区间上是单调的,则该 区间称为函数的单调区间
证 , ( , ), x1 x2 a b , 且 x1 x2 应用拉氏定理,得 ( ) ( ) ( )( ) ( ) 2 1 x2 x1 x1 x2 f x − f x = f − 0, x2 − x1 若在(a,b)内,f (x) 0, 则 f ( ) 0, ( ) ( ). 2 x1 f x f y = f (x)在[a,b]上单调增加. 若在(a,b)内,f (x) 0, 则 f ( ) 0, ( ) ( ). 2 x1 f x f y = f (x)在[a,b]上单调减少. 如果函数在其定义域的某个区间上是单调的,则该 区间称为函数的单调区间

少例1讨论函数y=e*一x-1的单调性. 解D:(-o,+o).y'=e-1. 在(-0,0)内,y'<0, 函数单调减少; 剂 在(0,+o)内,y>0,∴.函数单调增加
例 1 解 讨论函数y = e − x − 1的单调性. x = − 1. x y e 在 (−,0 ) 内, y 0, 函数单调减少; 在(0,+)内, y 0, 函数单调增加. D : ( , ). − +