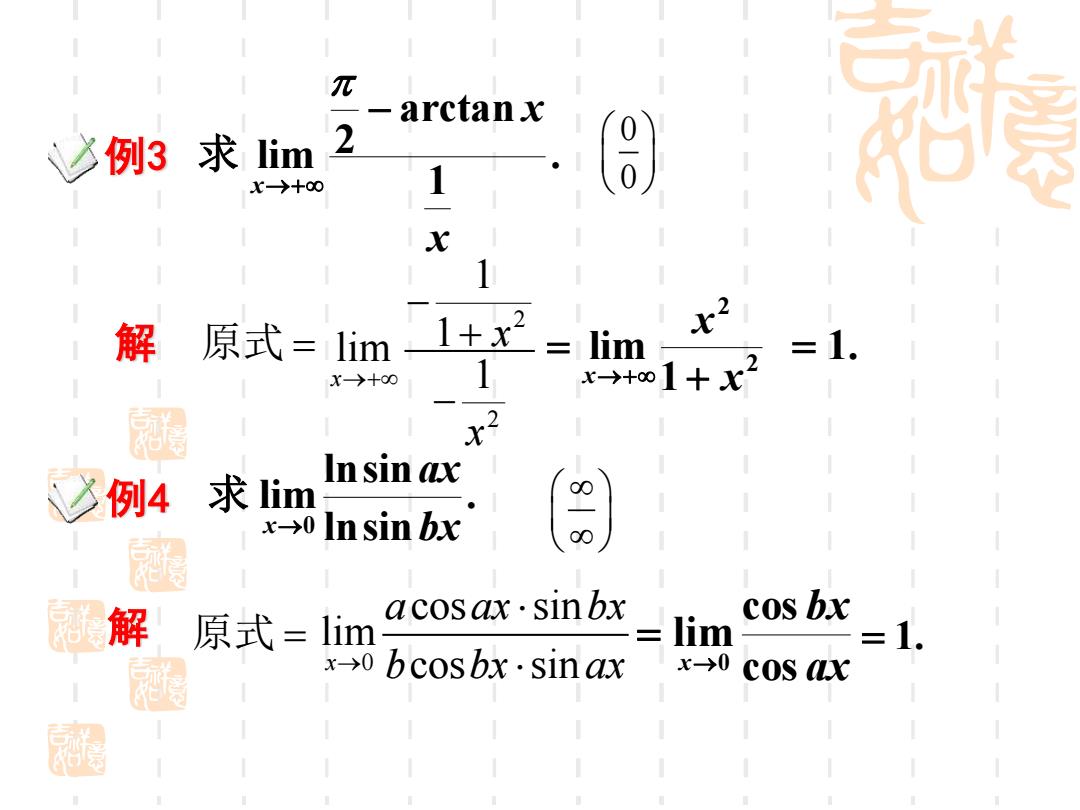
π arctanx 例3求lim 2 x→十00 1 X 1 解 原式=lim1+x2=lim x 1. X→+00 1 +x2 In sin ax 少例4 求lim x→0 Insin bx 解 ac0Sax·S1nbx -1im cos bx 原式=lim 1. x-0 bcosbx·sinax x-0 cos ax 翻
例 3 解 . 1 arctan 2 lim x x x − →+ 求 2 21 1 limx 1 x x →+ − + − 2 2 1 lim x x x + = →+ = 1 . 例 4 解 . lnsin lnsin lim0 bx ax x → 求 0 cos sin limx cos sin a ax bx → b bx ax = 1. 00 ax bx x cos cos lim→0 = 原 式 = 原 式 =

5求a>, 解原式=li n.xm-1 nxm lim X→十0 alnax. 1 X-→+0 o a Ine-!x X n2x” lim x→+oa(a-1)lna-2x =十00
例 5 解 ( 0). ln lim →+ x x n x 求 1 1 lim 1 ln n x n x x x − →+ − = 原式 = + . 1 lim . ln n x n x x →+ − = 2 2 lim ( 1)lnn x n x x →+ − = −

(二)0.0,0-0,0°,1,0°型未定式解法 关键:将其它类型未定式化为洛必达法则可解决的类型 00 求imx"e*. 1.00型 X→+00 步骤:00→ 0 0.00→-00, 例6 求limx2e*.(0oo) x→十0 解原式=im ex e lim lim =十00. X→+00 2x X→+0 2 X→+0 2
0 0 0 , , 0 ,1 , (二) − 型未定式解法 例6 解 lim . 2 x x x e − →+ 求 ( 0 ) x e x x 2 lim →+ 原式 = 2 lim x x e →+ = 2 lim x x e →+ = = +. 关键:将其它类型未定式化为洛必达法则可解决的类型 0 , 0 1. 0 型 步骤: , 1 0 1 0 0 . 0 lim . n x x x e − →+ 求
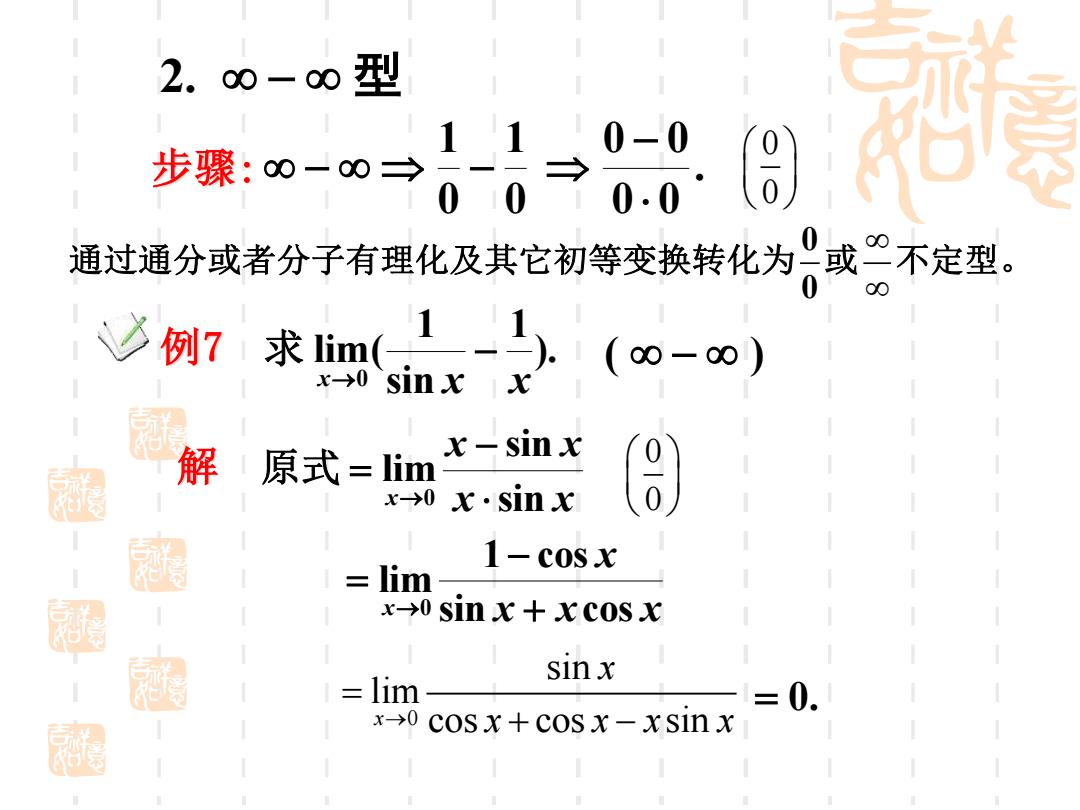
2.00-00型 1 步骤:0一00→ 0 通过通分或者分子有理化及其它初等变换转化为。或°不定型。 0 0 例7求imL.(0-0) x->0sin x x 冠 涵 解 原式=im -sinx x-→0x.sinx 8 1-cosx 极腿 lim x→0sinx+xCOSx sinx =lim =0. x-0 COSx+coSx-xsinx
例7 解 ). 1 sin 1 lim( x 0 x x − → 求 ( − ) 0 1 0 1 − − . 0 0 0 0 − x x x x x sin sin lim 0 − = → 原式 x x x x x sin cos 1 cos lim 0 + − = → = 0. 2. − 型 步骤: 0 0 0 0 0 sin lim x cos cos sin x → x x x x = + − 0 0 通过通分或者分子有理化及其它初等变换转化为 或 不定型

3.0°,1,0°型 步骤: 0° 0.ln0 10 0alm→0oo.三 取对数 或 00 0 0.Inco 通过[f(x)()=ex)mfx)将三种不定式转化为0.oo型 之例8求1imx2.(0°)(0.∞) x-→>0+ 2 lim lim 2xInx x→0+ 1 解 原式=lime2xmx=ex+ 00 e x-→0+ 1 2 lim r x→0+ 1 e 0 =1
步骤: 0 0 0 , 1 , 3. 型 0 0 0 0 ln 0 1 ln1 0 ln ⎯⎯⎯→ 取对数 0 . 例8 解 2 0 lim . x x x 求 → + ( 0 ) 0 2 ln 0 lim x x x e → + 原式 = 0 lim 2 ln x x x e → + = 0 2 1 2 lim 1 x x x e → + − = 0 = e = 1. 0 ln 2 lim 1 x x x e → + = 0 0 或 (0) ( ) ( )ln ( ) [ ( )]g x g x f x 通过 f x e = 将三种不定式转化为0 型