《线性代数》课程教学资源（讲稿B，高教版）第三章 n维向量空间 3-3 向量组的秩与极大无关组

行初等变换→B,若A定理1则A的任意k个(1≤k≤n)个列向量与B的对应k个列向量有相同的线性相关性行初等变换证>BkA任取A的k个列向量所得AkX=0与BkX=0同时有非零解或只有零解A,的列向量与B,的列向量有相同的线性相关性加油！

B 的对应 k 个列向量有相同的线性相关性. 定理1 若 证 任取A的k个列向量所得 Ak X = 0 与 Bk X = 0 同时有非零解或只有零解. Ak 的列向量与 Bk 的列向量有相同的线性相关性. , A B m n  行初等变换 , A B k k  行初等变换 则A的任意 k个( 1≤ k ≤ n)个列向量与

结论1：行（列）初等变换不改变矩阵列（行）向量间的线性关系30112-1例设矩阵A=050246列向量αi,αz,α3,α,间有线性关系α=α,+2α,-α加油！

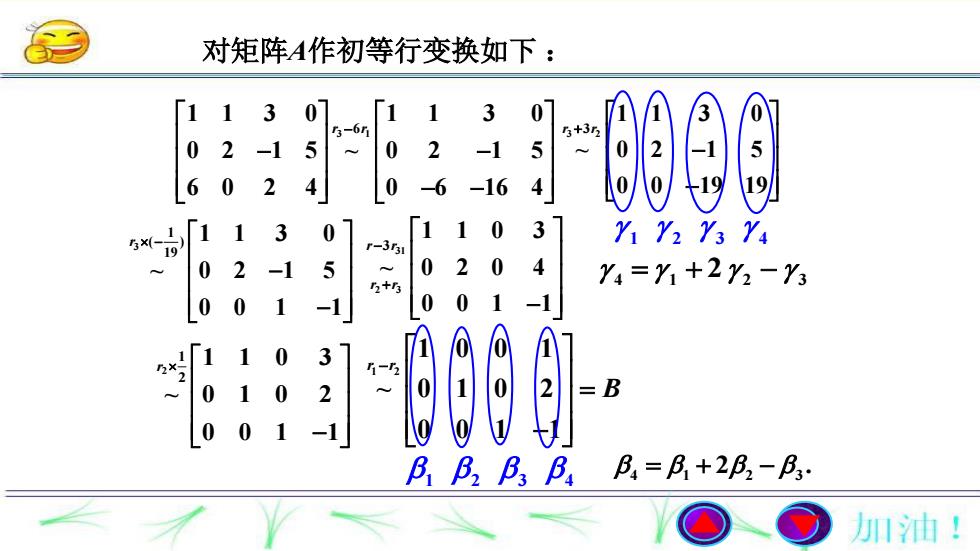
结论1：行（列）初等变换不改变矩阵列（行）向量间的线性关系. 1 1 3 0 0 2 1 5 6 0 2 4 例 设矩阵A             1 2 3 4 4 1 2 3 , 2            列向量 间有线性关系

对矩阵A作初等行变换如下：3031I31+3r250511916-16431 2 3 4031940514 = X1 +2 2 -3?01202=B20-2福001β, =β, +2β, -β3β β, β, β加油！

对矩阵A作初等行变换如下 ： 3 1 6 1 1 3 0 1 1 3 0 0 2 1 5 ~ 0 2 1 5 6 0 2 4 0 6 16 4 r r                          3 2 3 1 1 3 0 ~ 0 2 1 5 0 0 19 19 r r              3 1 ( ) 19 1 1 3 0 ~ 0 2 1 5 0 0 1 1 r               31 2 3 3 1 1 0 3 ~ 0 2 0 4 0 0 1 1 r r r r              1 2 3 4     2 1 2 1 1 0 3 ~ 0 1 0 2 0 0 1 1 r             1 2 1 0 0 1 ~ 0 1 0 2 0 0 1 1 r r B                  1 2 3 4 4 1 2 3        2 . 4 1 2 3        2

矩阵A的列秩：A的列向量组的秩：矩阵A的行秩：A的行向量组的秩结论2：初等行(列)变换不改变矩阵的列(行)秩加油！

矩阵A的列秩：A的列向量组的秩； 矩阵A的行秩：A的行向量组的秩. 结论2：初等行(列)变换不改变矩阵的列(行)秩

定理2矩阵的行秩=列秩=矩阵的秩证 设 R(A) = r， A=行初等变换>B(行阶梯形矩阵),B有r个非零行，B的r个非零行的非零首元素所在的r个列向量线性无关，为B的列向量组的极大无关组加油！

定理2 矩阵的行秩 = 列秩 = 矩阵的秩. 证 设 R(A) = r, A B  ( ), 行初等变换 行阶梯形矩阵 B有 r 个非零行，B的r 个非零行的非零首元素 所在的r 个列向量线性无关，为B的列向量组的 极大无关组