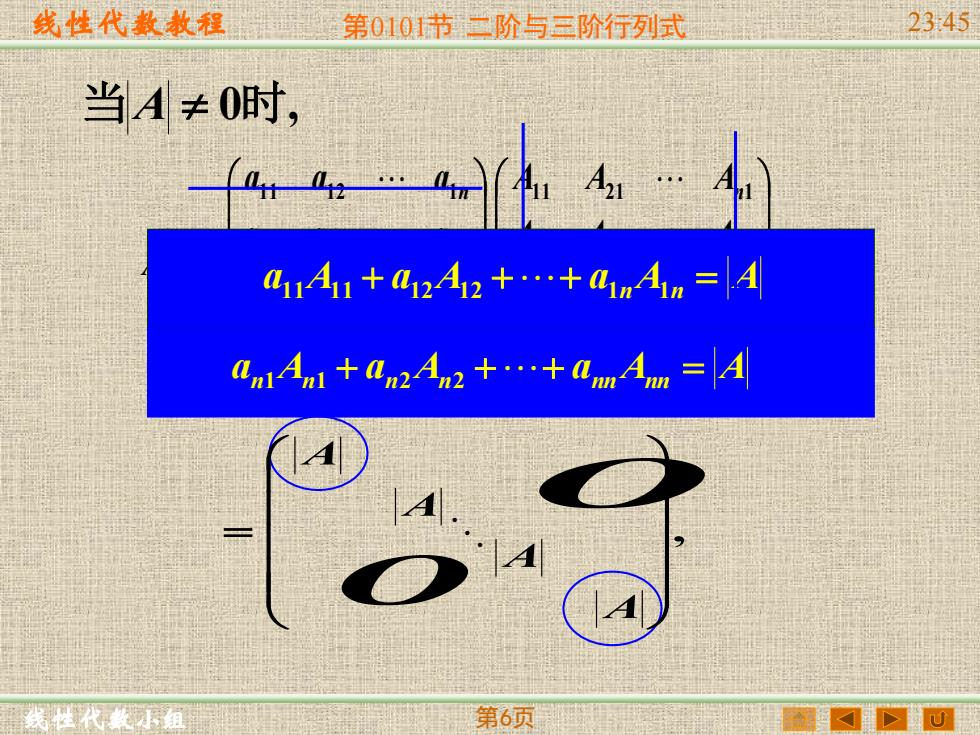
线性代教教程 第0101节三阶与三阶行列式 2345 当A≠0时, 411Al+a242+.+amAn=4 am An an2An2++am Am A 第6顾
线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:45 第6页 当A 0时, = n n nn n n n n nn n n A A A A A A A A A a a a a a a a a a AA 1 2 1 2 2 2 2 1 1 2 1 1 1 2 2 1 2 2 2 1 1 1 2 1 a11A11 + a12A12 ++ a1nA1n = A an1An1 + an2An2 ++ annAnn = A , = A A A A O O

线性代数敖程 第0101节二阶与三阶行列式 23:45 AA-AA-AE-A4-4A-E 按逆矩阵的定义得 A 求逆矩阵的 证毕 方法之一 奇异矩阵与非奇异矩阵的定义 当|A=0时,A 由此可得A是可逆阵的充要条件是 A为非奇异矩阵 第7项
线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:45 第7页 AA = A A = AE A E, A A A A A = = . 1 A A A − = 按逆矩阵的定义得 证毕 奇异矩阵与非奇异矩阵的定义 . 为非奇异矩阵 由此可得 是可逆阵的充要条件是 A A 当 | A|= 0 时, A 求逆矩阵的 方法之一

线性代数故程 第0101节二阶与三阶行列式 2345 推论若AB=E(或BA=E),则B=AI 证明 AB=E-1,A≠0, 因而存在,于是 B=EB=(A'A)B=A'(AB) -E-N 逆矩阵的运算性质 (1)若A可逆,则A亦可逆,且(4)'=A 第8页
线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:45 第8页 A B = E = 1, A 0, , 1 因而 存在 − A 于是 B = EB (A A)B −1 = A (AB) −1 = A E −1 = . −1 = A ( ), . −1 推论 若AB = E 或BA = E 则B = A 证明 逆矩阵的运算性质 , , ( ) . 1 1 1 A A A = A - 若 可逆 则 - 亦可逆 且 - (1)

线性代数教程 第0101节三阶与三阶行列式 23:45 (2)若A可逆,数入≠0,则24可逆,且 -之知 (3)若A,B为同阶方阵且均可逆,则AB亦可逆,且 (A B)=BA 证明 (AB)BA-)=A(BB-)A =AEA-=AA=E, .(AB)=BA-. 第9页
线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:45 第9页 ( ) 2 若A可逆,数 0,则A可逆,且 ( )( ) ( ) −1 −1 −1 −1 AB B A = A BB A −1 = AEA , 1 = AA = E − ( ) . −1 −1 −1 AB = B A 证明 ( ) = −1 A B B −1 −1 A ( ) . −1 1 −1 A = A (3)若 A,B 为同阶方阵且均可逆 , 则 AB 亦可逆 ,且