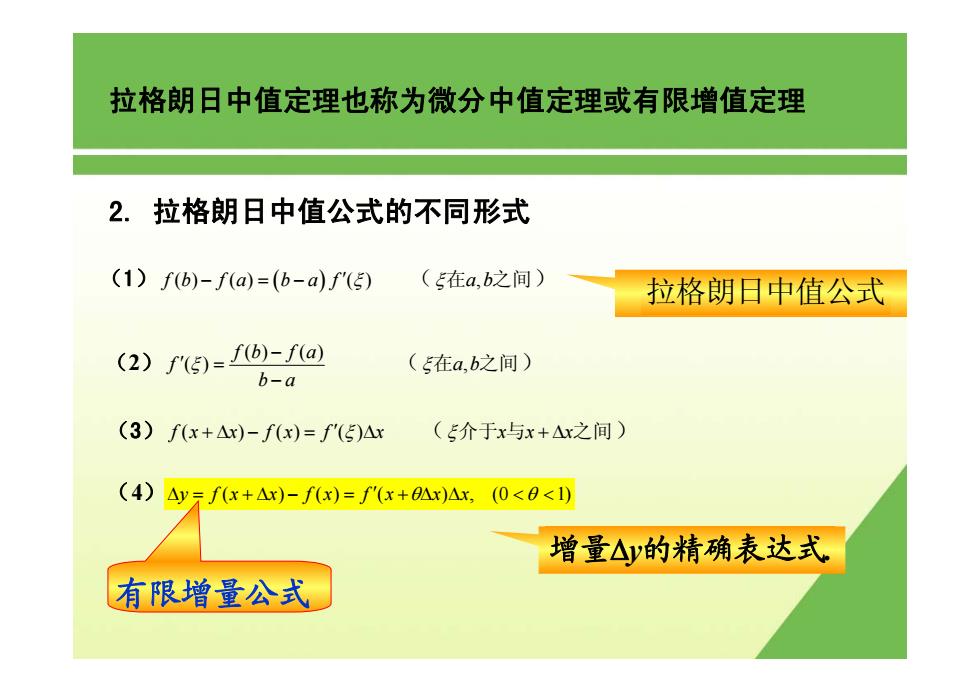
拉格朗日中值定理也称为微分中值定理或有限增值定理 2. 拉格朗日中值公式的不同形式 (1)fb)-f(a)=(b-a)f'(5) (5在a,b之间) 拉格朗日中值公式 (2)f5⑤)=fb)-f@ (5在a,b之间) b-a (3)f(x+△x)-fx)=f'(5)△x (E介于x与x+△x之间) (4)△y=f(x+△x)-f(x)=f'(x+孤x)△x,(0<0<1) 增量△y的精确表达式 有限增量公式
2. 拉格朗日中值公式的不同形式 ( 2 ) () () ( ) f b fa f b a ξ − ′ = − ( ξ在 之间 a b, ) (1) fb fa b a f () () () − =− ( ) ′ ξ ( ξ在 之间 a b, ) ( 4 ) Δy fx x fx f x x x = +Δ − = + Δ Δ < < ( ) ( ) ( ) , (0 1) ′ θ θ 有限增量公式 增量 Δy的精确表达式. (3) f ( ) () () x x + Δ− = Δ f x f ′ ξ x ( ξ介于 与 之间 xx x + Δ ) 拉格朗日中值公式 拉格朗日中值定理也称为微分中值定理或有限增值定理
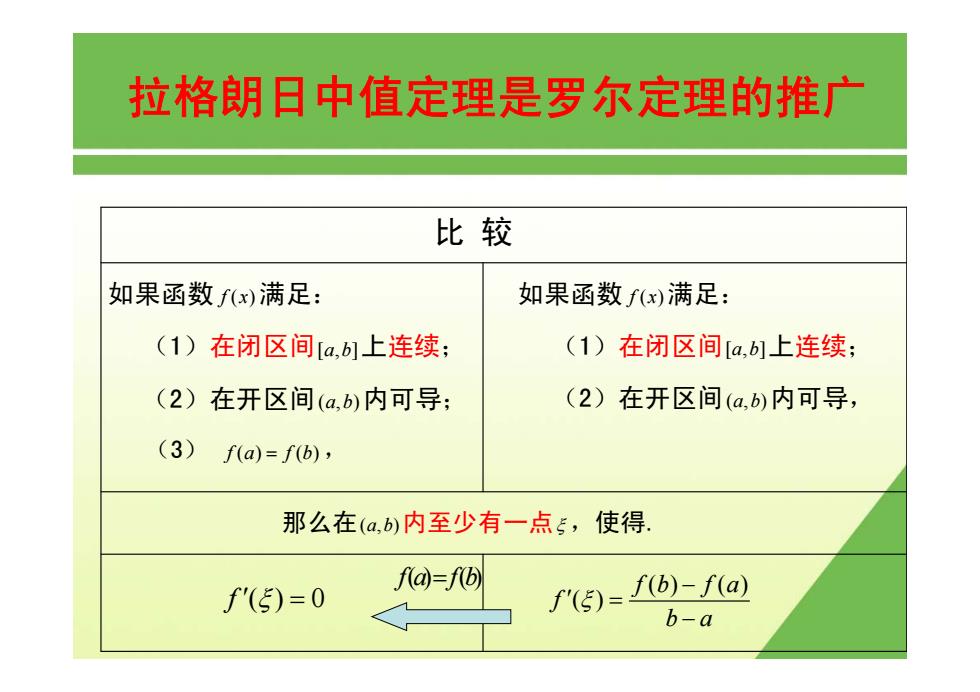
拉格朗日中值定理是罗尔定理的推广 比较 如果函数fx)满足: 如果函数f(x)满足: (1)在闭区间[a,b1上连续: (1)在闭区间[a,b1上连续; (2)在开区间(a,b)内可导: (2)在开区间(a,b)内可导, (3) f(a)=f(b), 那么在(a,b)内至少有一点5,使得. f@=f⑤ f'(5)=0 M)=I(b)-I(a) b-a
拉格朗日中值定理是罗尔定理的推广 比 较 如果函数 f ( ) x 满足: (1)在闭区间[,] a b 上连续; (2)在开区间(,) a b 内可导; (3) f () () a = f b , 那么在(,) a b 内至少有一点 ξ ,使得. f ′() 0 ξ = 如果函数 f ( ) x 满足: (1)在闭区间[,] a b 上连续; (2)在开区间(,) a b 内可导, () () ( ) f b fa f b a ξ − ′ = − fa fb () () =

三、拉格朗日中值定理 3.拉格朗日中值定理的几何意义 在两个高度不相同的点之间的连续曲线上若除端点外, 每一点都有不垂直于轴的切线,则其中必 有一条切线平行于两个端点的连线
3. 拉格朗日中值定理的几何意义 在两个高度不相同的点之间的连续曲线上若除端点外, 每一点都有不垂直于轴的切线,则其中必 有一条切线平行于两个端点的连线 三 、拉格朗日中值定理

三、拉格朗日中值定理 推论:如果f(x)在区间1的导数为零,那么x在区间/上为常数 分析 在区间上任取两点x<x f'(x)=0 拉格朗日中值定理 f(x2)-f(x)=f'(5x2-x) f'(5)=0 f(x,)=f(x) 见 因为x,x是1上任意两点,fx)在区间1上是一个常数
分析 在区间上任取两点 1 2 x x < ( ) ( ) ( )( ) 2 1 2 1 f x − f x = f ′ ξ x − x 拉格朗日中值定理 f x ′() 0 = f ′() 0 ξ = 2 1 fx fx () () 0 − = 2 1 f () () x fx = 因为 1 2 x x, 是I 上任意两点, f ( ) x 在区间I 上是一个常数 4. 推论:如果 f ( ) x 在区间I 的导数为零,那么 f ( ) x 在区间I 上为常数 三、拉格朗日中值定理

三、拉格朗日中值定理 注记5应用拉格朗日中值定理的推论证明在区间1上fx)=C的步骤 第一步:写出fw)的表达式 第二步:证明在区间1上f(x)=0 第三步:证明在区间1上有一点x,使得fx)=C
注记 5 应用拉格朗日中值定理的推论证明在区间 I 上 f ( ) x C= 的步骤 第一步:写出 f ( ) x 的表达式 三 、拉格朗日中值定理 第二步:证明在区间 I 上 f x ′() 0 ≡ 第三步:证明在区间 I 上有一点 0 x 使得 0 f ( ) x C=