三、拉格朗日中值定理 如果函数f(x)满足: (1)在闭区间[a,b]上连续; (2)在开区间(a,b)内可导, 那么在(a,b)内至少有一点5,使等式 Bagrang f(b)-f(a)=(b-af'(5) 成立. 拉格朗日中值 定理
如果函数 f x( )满足: (1)在闭区间[,] a b 上连续; (2)在开区间(,) a b 内可导, fb fa b a f () () () − =− ( ) ′ ξ 那么在(,) a b 内至少有一点ξ ,使等式 成立. 三、拉格朗日中值定理 拉格朗日中值 定理
拉格朗日中值定理结论分析 要证明结论我们只要证明 f()-I(b)-f(a)=0 b-a f"(E)-b)=f@=f'5)-fb)-f@x1 b-a b-a 我们只要证明 导数的运算法则 f(b)-f(a) le-0 '(5)- f(b)-f(a) (b)-f(a)x b-a b-a f(x)-i b-a x=5 作辅助函数()=fx)-Ib)-f@x 也就是要证明 b-a (1) p(x)在[a,b1上连续 只要证明o'(5)=0 (2)px)在(a,b)上可导 (3)p(a)=p(b) 只要证明函数(x)满足罗尔定理条件即可
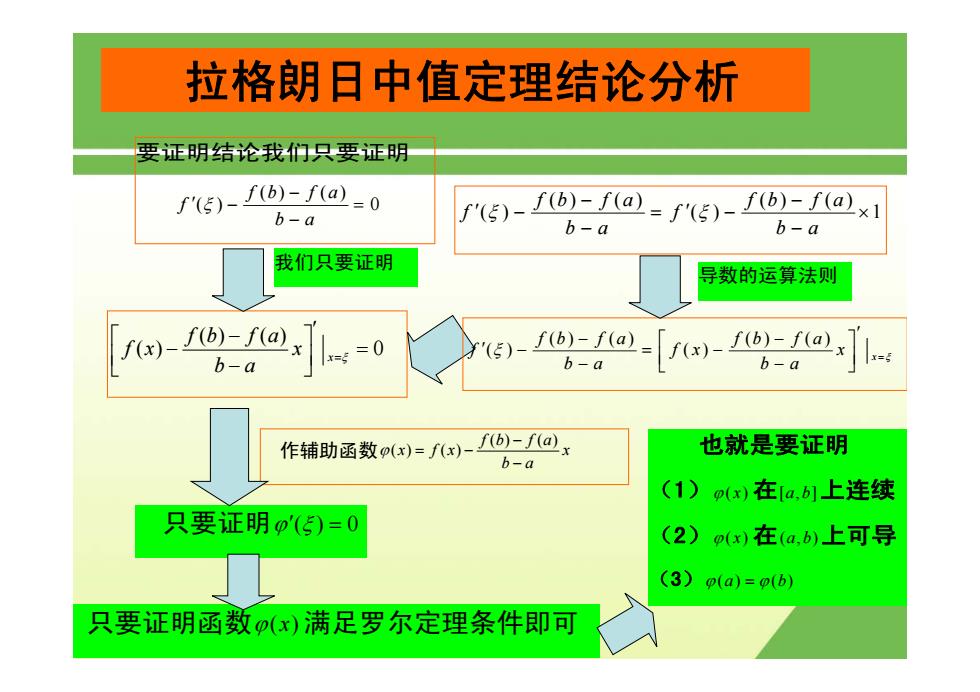
拉格朗日中值定理结论分析 导数的运算法则 作辅助函数 () () () () f b fa x fx x b a ϕ − = − − 只要证明 ϕ′() 0 ξ = () () () 0 x fb fa fx x b a = ξ ′ ⎡ ⎤ − − = ⎢ ⎥ ⎣ ⎦ − 要证明结论我们只要证明 () () () 0 fb fa f b a ξ − ′ − = − 只要证明函数 ϕ( ) x 满足罗尔定理条件即可 () () () () () () 1 fb fa fb fa f f ba ba ξ ξ − − ′ ′ − =− × − − 我们只要证明 () () () () () () x fb fa fb fa f fx x ba ba ξ ξ = ′ − − ⎡ ⎤ ′ − =− ⎢ ⎥ − − ⎣ ⎦ 也就是要证明 (1) ϕ ( ) x 在[,] a b 上连续 (2) ϕ ( ) x 在(,) a b 上可导 (3) ϕ () () a b = ϕ
拉格朗日中值定理证明分析 令0(x)fx)-Ib-f@, 由于函数/6x)满足 b-a (1)在闭区间[a,b1上连续 (2)在开区间(a,.b)内可导 a)=f(a)-I(b)-f(@a=bf(a)-a(b) b-a b-a (b)=f(b)-f(b)-f(a)b= bf(a)-af(b) (1)p(x)在[a,b1上连续 b-a b-a (2)p(x)在(a,b上可导 (3)p(a)=p(b) 由罗尔定 理可知 至少存在一个5e(a,b) 使得0'(飞)=0 至少存在一个5e(a,b)使得f'(5)- f(b)-f(a)=0 b-a
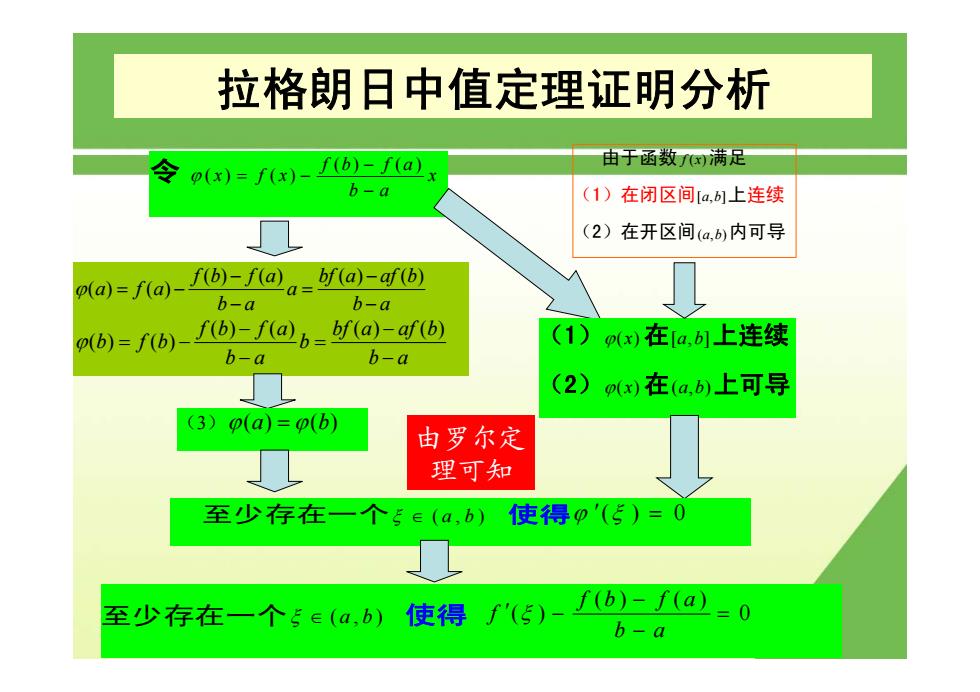
令 () () () () f b fa x fx x b a ϕ − = − − 拉格朗日中值定理证明分析 由于函数 f ( ) x 满足 (1)在闭区间[,] a b 上连续 (2)在开区间(,) a b 内可导 (1)ϕ( ) x 在[,] a b 上连续 (2)ϕ( ) x 在(,) a b 上可导 , () () () () () () f b f a bf a af b a fa a ba ba ϕ − − =− = − − () () () () () () f b f a bf a af b b fb b ba ba ϕ − − =− = − − (3)ϕ() () a b = ϕ 至少存在一个ξ ∈ (,) a b 使得ϕ ′() 0 ξ = 由罗尔定 理可知 至少存在一个ξ ∈ (,) a b 使得 () () () 0 fb fa f b a ξ − ′ − = −

三、拉格朗日中值定理 注记4:当a<b时,fb)-fa)=(b-a)f()成立 当a>b时,公式fb)-fa)=(b-a)f5)仍成立
注记 4: 当a b < 时, fb fa b a f () () () − =− ( ) ′ ξ 成立 三、拉格朗日中值定理 当a b > 时,公式 fb fa b a f () () () − =− ( ) ′ ξ 仍成立
f(b)-f(a)=(b-a)f'(E5) f(x+△x)-f(x)=f'(5)△x(5在x与x+△x之间) (1)当△x>0时 (2)当△r<0时 x<5<x+△x 令5=x+0△x x+△x<5<x 可 x<x+O.△x<x+△x x+△x<x+0·△x<x 贝 0<0·△x<△x △x<0·△x<0 0 <0 <1 0<0 <1 5=x+0.△x(0<0<1)
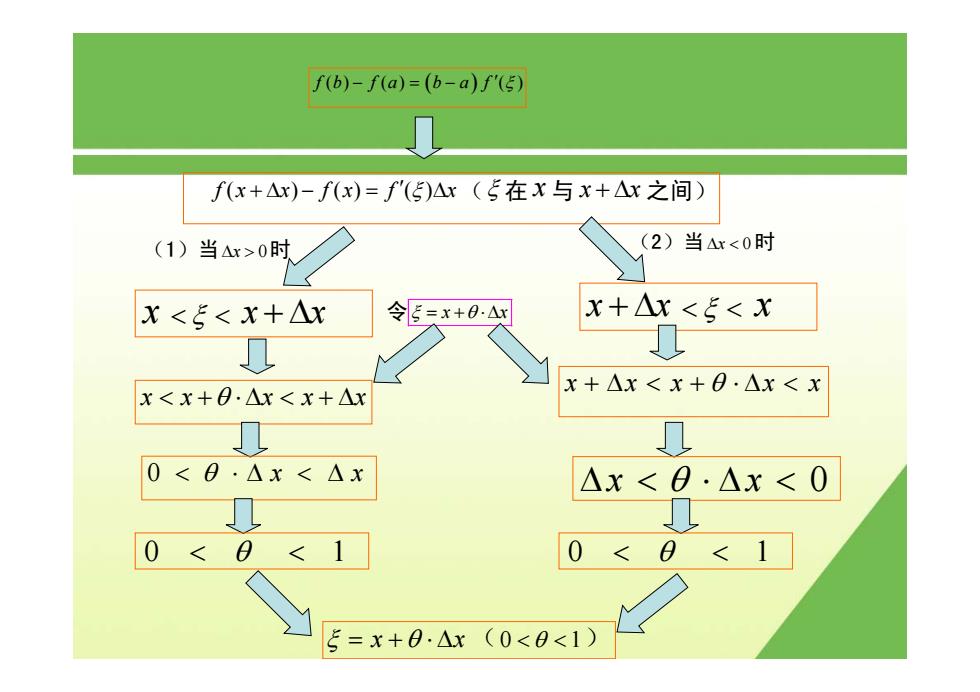
fb fa b a f () () () − =− ( ) ′ ξ fx x fx f x ( ) () () +Δ − = Δ ′ ξ (ξ 在 x 与 x x + Δ 之间) (1)当Δ >x 0时 x < ξ < x + Δx 令ξ = x x + ⋅Δ θ (2)当Δx < 0时 x + Δx < ξ < x x < x xx x + ⋅Δ < +Δ θ 0 < θ ⋅Δ < Δ x x 0 1 < θ < x + Δ < + ⋅Δ < xx xx θ Δx x < ⋅Δ < θ 0 0 1 < θ < ξ = x + ⋅Δ θ x (0 1 < θ < )