
第三章 中值定理与导数的应用 主要内容: 一、中值定理 二、洛必达法则 三、泰勒中值定理 四、函数的单调性与曲线的凹凸性 五、函数的极致与最值 五、函数图形的描绘
第三章 中值定理与导数的应用 主要内容 : 一、中值定理 二、洛必达法则 三、泰勒中值定理 四、函数的单调性与曲线的凹凸性 五、函数的极致与最值 五、函数图形的描绘

第三章 §3.1中值定理 主要内容: 一、极值概念及费马引理 二、罗尔中值定理 三、拉格朗日中值定理 四、柯西中值定理
二、罗尔中值定理 三、拉格朗日中值定理 四、柯西中值定理 §3.1 中值定理 第三章 一、极值概念及费马引理 主要内容:

一、极值概念及费马引理 1.极值的定义 设函数y=f(w)的定义域为D (1)都有fx)≤x,) (2)都有f(x)≥fx) 如果存在x的某一邻域 则称函数y=f(x)在 则称函数y=f(x)在 点x,处有极大值飞) 点x,处有极小值f) U(xo)cD,使得对任意的xeU(x) 点x称为极大值点. 点x,称为极小值点, 极大值和极小值统称为极值:极大值点和极小值点统称为极值点 注记1:若函数的最(大小)值在区间内部取得,则它一定是极值
一、极值概念及费马引理 1. 极值的定义 设函数 y f = ( ) x 的定义域为 D 如果存在 0 x 的某一邻域 0 Ux D ( ) ⊂ ,使得对任意 的 0 x ∈ U x( ) (1)都有 0 f () ( ) x ≤ f x 则称函数 y fx = ( ) 在 点 0 x 处有极大值 0 f ( ) x . 点 0 x 称为极大值点. (2)都有 0 f () ( ) x ≥ f x 则称函数 y fx = ( ) 在 点 0 x 处有极小值 0 f ( ) x . 点 0 x 称为极小值点. 极大值和极小值统称为极值;极大值点和极小值点统称为极值点 注记1: 若函数的最 ( 大小)值在区间内部取得,则它一定是 极值

一、极值概念及费马引理 2.费马引理 (1)若函数f)在点x,的某邻域U(x)内有定义,且在点,处可导 (2)函数fx)在点x,取到极值 则 f'(x)=0 我们把导数为零的点称为函数的驻点(或称稳定点,临界点) 注记2:可导函数的极值点一定是驻点
2. 费马引理 (2)函数 f ( ) x 在点 0 x 取到极值 则 (1)若函数 f ( ) x 在点 0 x 的某邻域 0 U x( )内有定义,且在点 0 x 处可导 0 f x ′()0 = 我们把导数为零的点称为函数的驻点(或称稳定点,临界点) 注记 2:可导函数的极值点一定是驻点. 一、极值概念及费马引理
费马引理的证明分析 不妨设xEU(x,)时fx)sfx),于是,对于x。+△xEU(x), L f(x+△x)f(x) 见 当△x>0时 △y=f(x+△x)-f(x)≤0 当Ax<0时 △y ∫(x)在点x。处可导 ≤0 △x △x 极限的保号性 f()=f)=f'() f(xo)=f(xo)=lim Ay 20 f(x)=f(xo)=lim ≤0 △r→0-△x 4x0△x f'(x)=0
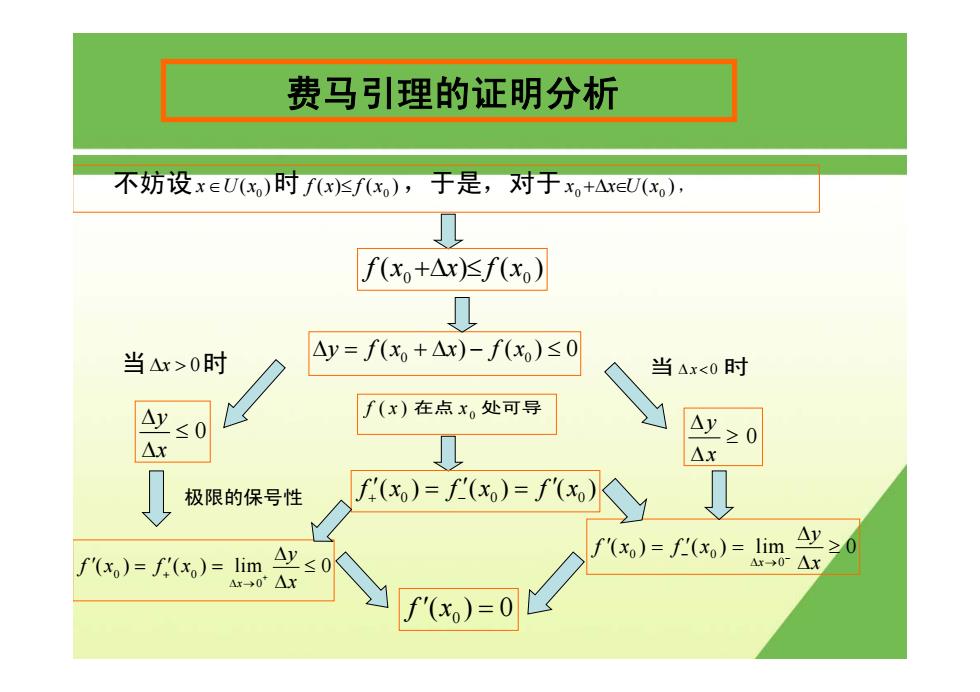
不妨设 0 x∈U x( )时 ( ) ( ) 0 f x ≤ f x ,于是,对于 ( ) 0 0 x +Δx∈U x , 费马引理的证明分析 ( ) ( ) 0 0 f x +Δx ≤ f x 当Δx > 0时 0 y x Δ ≤ Δ 0 0 0 ( ) ( ) lim 0 x y fx fx x + + Δ → Δ ′ ′ == ≤ Δ 0 y x Δ ≥ Δ 极限的保号性 当Δ x < 0 时 0 0 0 ( ) ( ) lim 0 x y fx fx x − − Δ → Δ ′ ′ = = ≥ Δ f ′(x0 ) = 0 0 0 Δy fx x fx = +Δ − ≤ ( ) ()0 f ( ) x 在点 0 x 处可导 0 00 f () () () x fx fx + − ′ = ′ ′ =