
第二节Euler方法 Euler方法 二 改进Euler方法 三、小结
第二节 Euler 方法 一 Euler 方法 三、小结 二 改进 Euler 方法

Euler方法 给定初值问题 y'=f(x,y) (1.1) y(x)= (1.2) 其中f(x,y)为x,y的已知函数,是给定的常数, 求(1.1)、(1.2)的数值解。 Eler方法是解初值问题(1.1)、(1.2)是简单 数值解法。由于它的精确度不高,实际计算中已 不被采用,然而它在苛种程度上却反映了数值解法 的基本思想
给定初值问题 其中 为 的已知函数, 是给定的常数, 求(1.1)、(1.2)的数值解。 f x y ( , ) x y, 0 y 一 Euler 方法 0 0 ( , ) ( ) y f x y y x y = = (1.1) (1.2) 方法是解初值问题(1.1)、(1.2)是简单 数值解法。由于它的精确度不高, 实际计算中已 不被采用,然而它在苛种程度上却反映了数值解法 的基本思想。 Euler
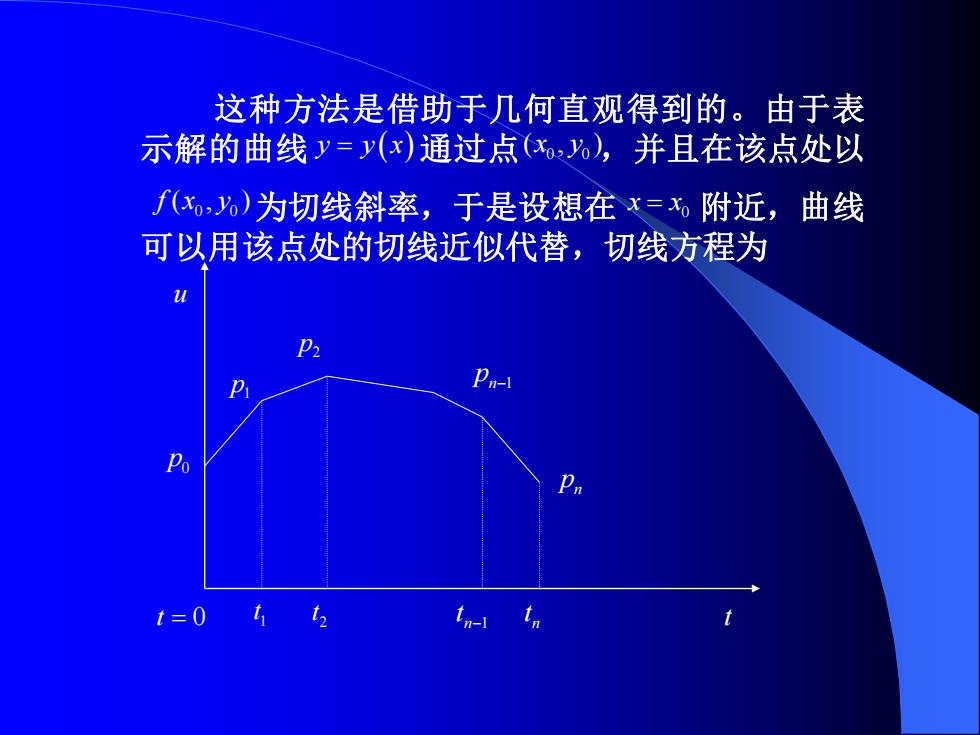
这种方法是借助于几何直观得到的。由于表 示解的曲线y=(x)通过点(x),并且在该点处以 (x,%)为切线斜率,于是设想在x=附近,曲线 可以用该点处的切线近似代替,切线方程为 u Pn- Po t=0 412 tn-1 In
0 p 1 p 2 p pn−1 n p t = 0 1 t 2 t n 1 t − n t u t 这种方法是借助于几何直观得到的。由于表 示解的曲线 通过点 ,并且在该点处以 为切线斜率,于是设想在 附近,曲线 可以用该点处的切线近似代替,切线方程为 0 0 ( , ) x y 0 0 f x y ( , ) 0 x x = y y x = ( )

y=yo +f(ao)(x-xo) 也就是说,x=x时,y=(x)可用+f(x,y)h近 似代替,记这个值为y,即 y=%+h时(x,%) 于是给出了一种当x=x时,获得函数值(x)的近 似值的方法。重复上面的作法,在x=x处,就 可以得到y(x2)的近似值 y2=y+hf(,)
0 0 0 0 y y f x y x x = + − ( , )( ) 也就是说, 时, 可用 近 似代替,记这个值为 ,即 1 x x = 1 y x = ( ) 0 0 0 y f x y h + ( , ) 1 y 1 0 0 0 y y hf x y = + ( , ) 于是给出了一种当 时,获得函数值 的近 似值 的方法。重复上面的作法,在 处,就 可以得到 的近似值 1 x x = 1 y x( ) 1 y 2 x x = 2 y x( ) 2 1 1 1 y y hf x y = + ( , )

依此下去,当y已经得到,则 ynt =yn+hf(nn) 这就是著名的Euler方法的计算格式。 由于uler方法是用一条折线近似地代替曲 线y(x),所以Eler方法也叫Eler折线法。 种计算格式,当在计算y时,仅仅用到 它前一步的信息y,称它为单步法。可见卫所法 就是单步法
1 ( , ) n n n n y y hf x y + = + 依此下去,当 yn 已经得到,则 这就是著名的 Euler 方法的计算格式。 Euler Euler 由于 方法是用一条折线近似地代替曲 线 y x( ) ,所以 Euler 方法也叫 折线法。 Euler n 1 y + n y 一种计算格式,当在计算 时,仅仅用到 它前一步的信息 ,称它为单步法。可见 方法 就是单步法