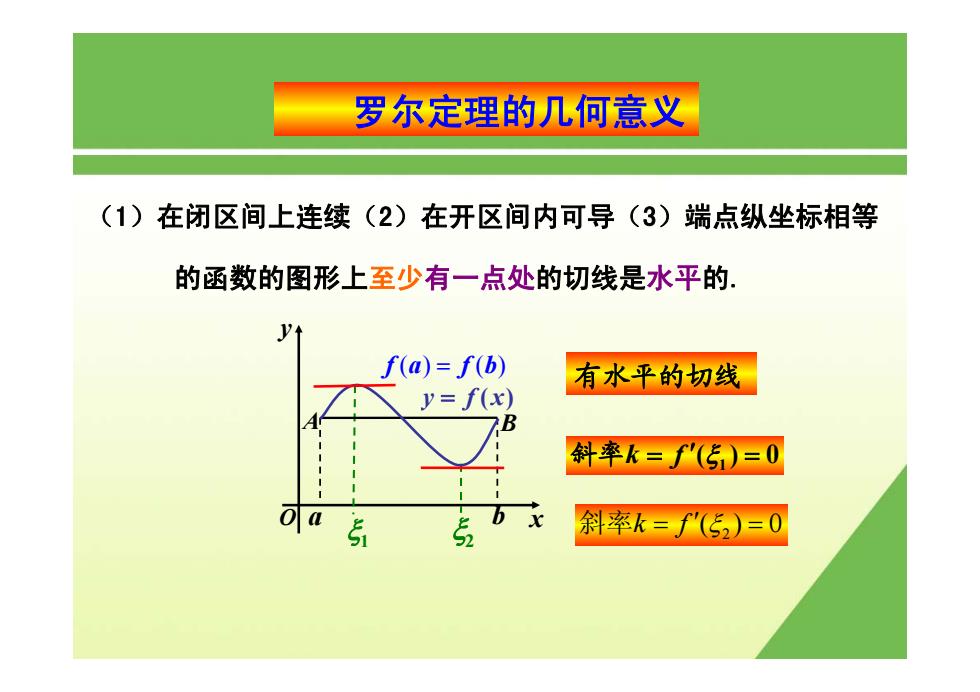
罗尔定理的几何意义 (1)在闭区间上连续(2)在开区间内可导(3)端点纵坐标相等 的函数的图形上至少有一点处的切线是水平的 f(a)=f(b) 有水平的切线 y=f(x) B 斜率k=f'(5)=0 斜率k=f'(52)=0
x y O ξ 1 ξ2 a b y = f (x) A B f (a) = f (b) 有水平的切线 斜率k = f ′(ξ 1 ) = 0 (1)在闭区间上连续(2)在开区间内可导(3)端点纵坐标相等 的函数的图形上至少有一点处的切线是水平的. 2 斜率k f = ′()0 ξ = 罗尔定理的几何意义
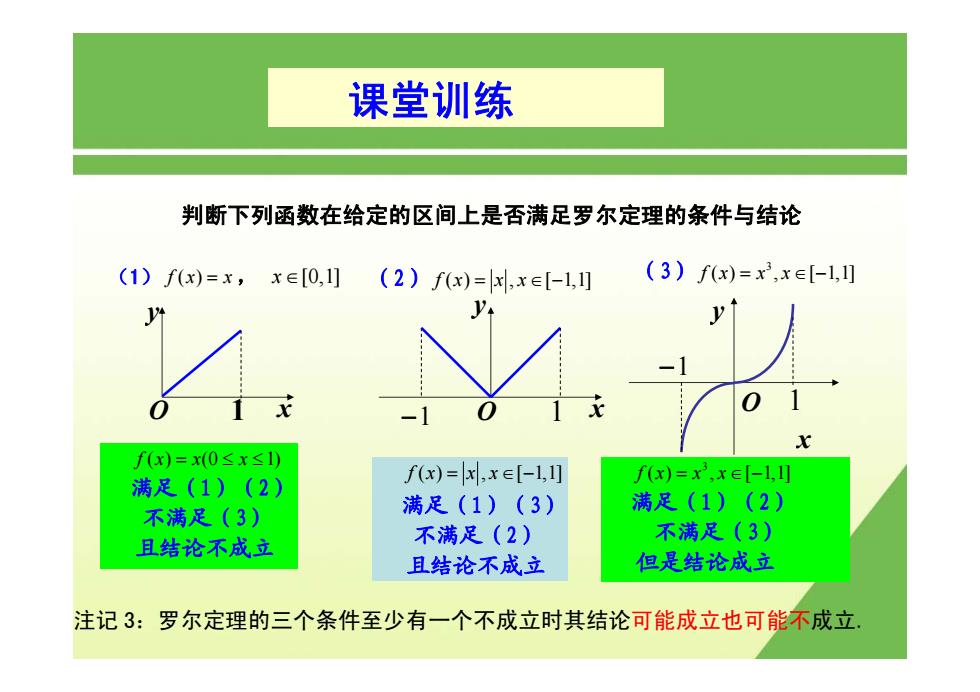
课堂训练 判断下列函数在给定的区间上是否满足罗尔定理的条件与结论 (1)fx)=x,x∈[0,1](2)fx)=x,x∈[-1,] (3)fx)=x,x∈-1,1 f(x)=x(0≤x≤1 满足(1)(2) f(x)=x,x∈[-l,1] fx)=x3,xe[-1,11 满足(1)(3) 满足(1)(2) 不满足(3) 不满足(3) 且结论不成立 不满足(2) 且结论不成立 但是结论成立 注记3:罗尔定理的三个条件至少有一个不成立时其结论可能成立也可能不成立
判断下列函数在给定的区间上是否满足罗尔定理的条件与结论 课堂训练 (1) f ( ) x x = , x ∈[0,1] (2) fx xx ( ) , [ 1,1] = ∈− (3) 3 fx x x ( ) , [ 1,1] = ∈− y x O − 1 1 − 1 y 1 x O 1 x y O fx x x ( ) (0 1) = ≤ ≤ 满足(1)(2) 不满足(3) 且结论不成立 fx xx ( ) , [ 1,1] = ∈− 满足(1)(3) 不满足(2) 且结论不成立 3 fx x x ( ) , [ 1,1] = ∈− 满足(1)(2) 不满足(3) 但是结论成立 注记 3:罗尔定理的三个条件至少有一个不成立时其结论可能成立也可能不成立

二、 罗尔定理 例2:不管b取何值,方程x3-3x+b=0在(-1,1)上至多有一个实解 解:设f(x)=x3-3x+b假设方程f(x)=0有两个实解x,x2∈(-1,1), -1<x1<x2<1. 显然f(x)在[x,x2]上连续,在(x,x2)上可导,且f(x)=f(x2)=0 由罗尔定理可知,至少存在一个5∈(x,x2)使得f'(5)=0 但当-1<x<5<x2<1时f'(5)=352-35=3(5-1)(5+1)<0 矛盾.故假设不成立,因此命题真
例 2:不管b 取何值,方程 3 x xb −3 0 + = 在( 1,1) − 上至多有一个实解. 解:设 3 f () 3 x x xb =−+ 假设方程 f x() 0 = 有两个实解 1 2 x x, ( 1,1), ∈ − 1 2 −1 1. <<< x x 由罗尔定理可知,至少存在一个 1 2 ξ ∈(, ) x x 使得 f ′() 0 ξ = 但当 1 2 −< < < < 1 1 x x ξ 时 2 f ′( ) 3 3 3( 1)( 1) 0 ξξξξξ = − = − +< 显然 f ( ) x 在 1 2 [, ] x x 上连续,在 1 2 (, ) x x 上可导,且 1 2 fx fx () () 0 = = 矛盾.故假设不成立.因此命题真. 二、罗尔定理

二、罗尔定理 例3:判断正误 1.设f(x)=x(x0-1),则方程f"(x)=0在(0,1)内至少有一个实根 2. 设f(x)=xsinx,则当x∈(0,π)时曲线y=xsinx.上至少有一点的 切线是水平的
例 3:判断正误. 1. 设 100 10 fx x x ( ) ( 1) = − ,则方程 f x ′() 0 = 在(0,1) 内至少有一个实根. 2. 设 f ( ) sin xxx = ,则当 x∈(0, ) π 时曲线 y = x x sin 上至少有一点的 切线是水平的. 二、罗尔定理
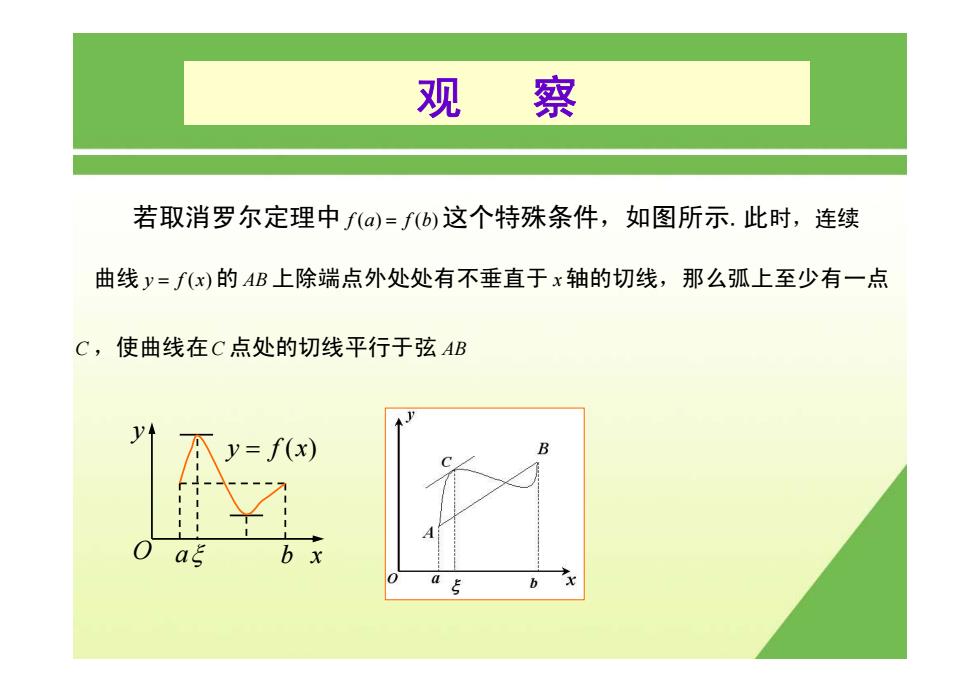
观察 若取消罗尔定理中f()=fb)这个特殊条件,如图所示.此时,连续 曲线y=f(x)的AB上除端点外处处有不垂直于x轴的切线,那么弧上至少有一点 C,使曲线在C点处的切线平行于弦AB y=f(x) ag b x
观 察 若取消罗尔定理中 fa fb () () = 这个特殊条件,如图所示.此时,连续 曲线 y f = ( ) x 的 AB 上除端点外处处有不垂直于 x 轴的切线,那么弧上至少有一点 C ,使曲线在C 点处的切线平行于弦 AB ξ x y a b y = f (x) O