§10.3 幂级数 函数项级数的概念 幂级数及收敛区间 幂级数的运算
§10.3 幂级数 函数项级数的概念 幂级数及收敛区间 幂级数的运算
函数项级数及其有关的概念 函数项级数的概念 函数项级数的收敛域 给定一个定义在区间I上的函数列 o∈I ∑4(x)收敛 (x)发散 4(x),山2(x),…,山n(x),…,则式子 4(x)+4(x)+…+un(x)+… x称为 xo称为 收敛点 发散点 称为区间I上的函数项级数,记作 ∑u.( 即 ∑4,()=4(x)+4,()+…+,(x)+. =1+++ 函数项级数“, 函数项级数u,(x) n=1 如 n=1 所有收敛点集合 所有发散点集合 显然r 称为收敛域 称为发散域 的收敛域为(-1,1) n=1
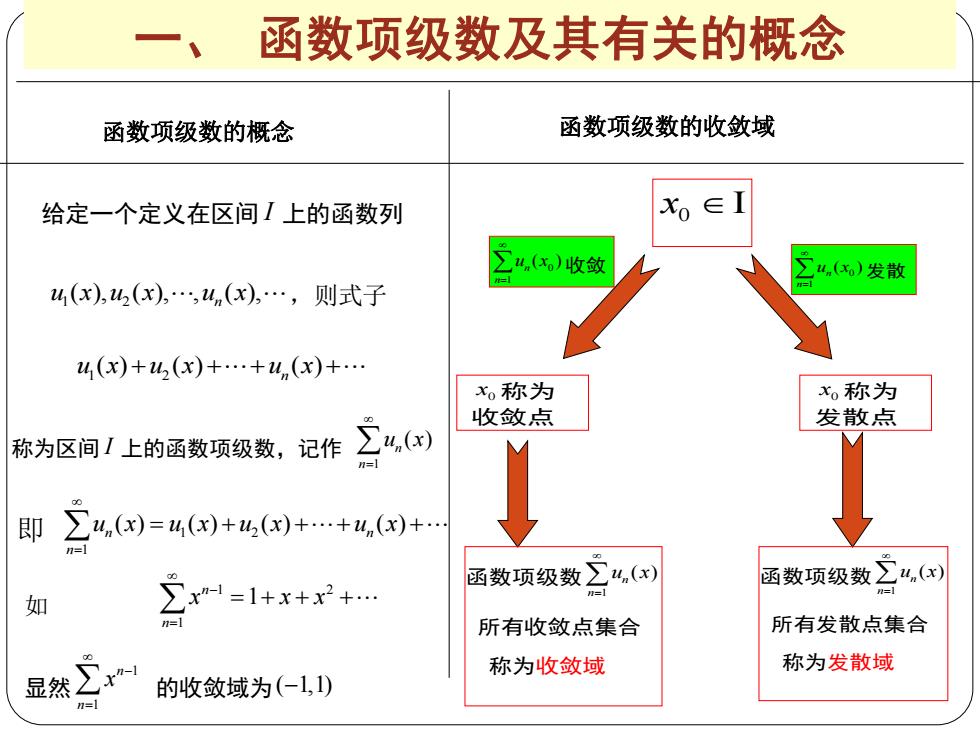
一、 函数项级数及其有关的概念 函数项级数的概念 函数项级数的收敛域 给定一个定义在区间 I 上的函数列 1 2 ( ), ( ), , ( ), n u x u x u x ,则式子 1 2 ( ) ( ) ( ) u x u x u x n 称为区间 I 上的函数项级数,记作 1 ( ) n n u x 即 1 2 1 ( ) ( ) ( ) ( ) n n n u x u x u x u x 如 1 2 1 1 n n x x x 0 x 0 1 ( ) n n u x 收敛 x0 称为 收敛点 0 1 ( ) n n u x 发散 x0 称为 发散点 函数项级数 1 ( ) n n u x 所有收敛点集合 称为收敛域 函数项级数 1 ( ) n n u x 所有发散点集合 称为发散域 显然 1 1 n n x 的收敛域为( 1,1)

二 幂级数及收敛域 幂级数的概念 幂级数的收敛域 上a-称为的幂级数 定理1:幂级数,x:的收敛性为下列三种情形之一 (1)在(-0,+∞)内处处绝对收敛 41,42,…,an…称为幂级数 (称它的收敛半径R=+0,(-∞,+∞)是它的收敛域) 的系数,是常数 2)仅在x=0处收敛; 当。=0时, 称为x的幂级数 (称它的收敛半径R=0,它的收敛域为一个点x=0 (3)存在确定的正数R,当<R时绝对收敛, 令1=-元时,幂级数立a,(x-x 当>R时发散. 就转化为幂级数a (称它的收敛半径为R,收敛区间为(一R,R), 收敛域为四种之一:(-RR),(←R,R,-R,R),[一RR]
二、 幂级数及收敛域 幂级数的概念 幂级数的收敛域 0 0 n n n a x x 称为( ) 0 x x 的幂级数 1 2 , , , n a a a 称为幂级数 的系数,是常数 当 0 x0 时, 0 n n n a x 称为 x 的幂级数. 令 0 t x x 时,幂级数 0 0 n n n a x x 就转化为幂级数 0 n n n a t 定理 1:幂级数 0 n n n a x :的收敛性为下列三种情形之一: (1)在(,)内处处绝对收敛 (称它的收敛半径 R ,(,) 是它的收敛域) (2)仅在 x 0处收敛; (称它的收敛半径R 0,它的收敛域为一个点 x 0) (3)存在确定的正数 R ,当 x R 时绝对收敛, 当 x R 时发散. (称它的收敛半径为 R ,收敛区间为( , ) R R , 收敛域为四种之一:( , ), R R ( , ], R R [ , ), R R [ , ] R R
二 幂级数及收敛域 定理2 设幂级数∑a,r的系数满足 例1 求幂级数-)的收敛半径和收敛域 n=0 lim an*l上p 解 显然a=(-1) n-c0 an n 1 则这幂级数的收敛半径 因此 im卡limn+=l a. 1 D=0 所以p=1,故收敛半径为R==1 P≠0 0 p=+∞ 当x=1时,幂级数成为2-是收敛的 第一步:确定幂级数a,r的系数通项a 当x=-1时,幂级数成为是发散的 第二步:计算极限P 因此,幂级数立-1)的收敛域为-1,1]. 第三步:确定2ar的收敛半径 = 第四步: 确定三x的收敛域
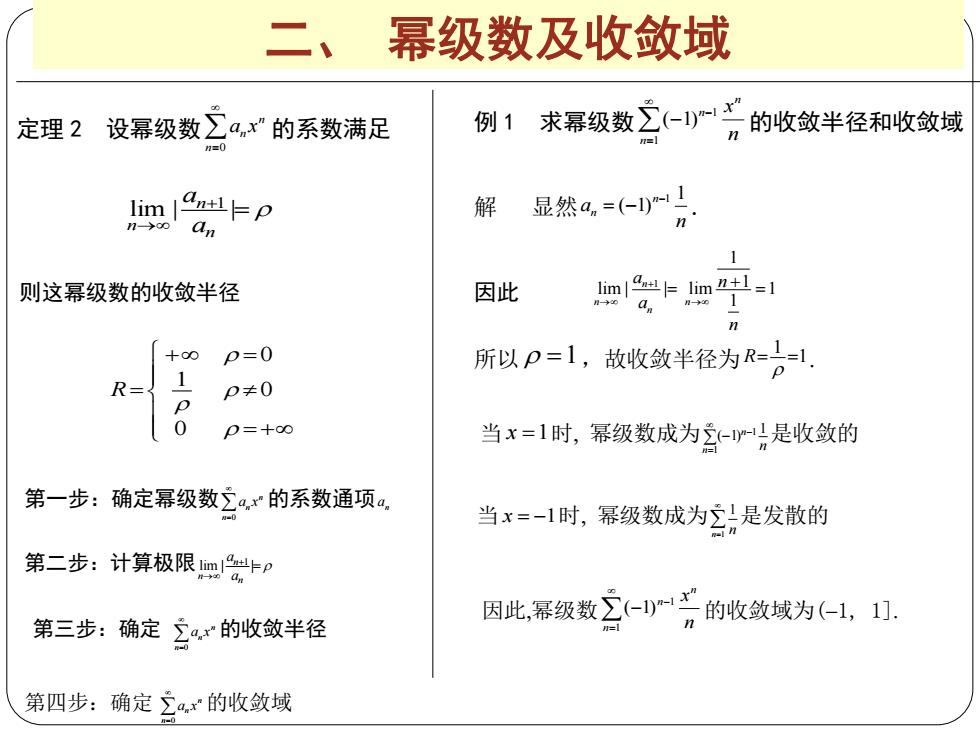
二、 幂级数及收敛域 定理 2 设幂级数 0 n n n a x 的系数满足 lim | | 1 n n n a a 则这幂级数的收敛半径 0 0 1 0 R 例 1 求幂级数 1 1 ( 1) n n n x n 的收敛半径和收敛域 第一步:确定幂级数 0 n n n a x 的系数通项 n a 第二步:计算极限 lim | | 1 n n n a a 第三步:确定 0 n n n a x 的收敛半径 第四步:确定 0 n n n a x 的收敛域 解 显然 1 1 ( 1)n n a n . 因此 1 1 1 lim | | lim 1 1 n n n n a n a n 所以 1,故收敛半径为 1 1 R 当 x 1时 幂级数成为 1 1 1 ( 1) n n n 是收敛的 当 x 1时 幂级数成为 1 1 n n 是发散的 因此幂级数 1 1 ( 1) n n n x n 的收敛域为(1, 1]

二 幂级数及收敛域 定理2 设幂级数 r的系数满足 例2 求幂级数三 的收敛半径和收敛域 lim卡p 解 1n-→c0 an 显然a,=m 1 则这幂级数的收敛半径 因此 lmu卡limm+=lim1 =0 月→ a i-→on+1 n! +00 p=0 p≠0 所以p=0,故收敛半径为R=0. P D=+0 第一步:确定幂级数4,x的系数通项a, 因此,幂级数的收敛域为(-o,+o), 第二步:计算极限mp 第三步:确定2ar的收敛半径 第四步:确定ar的收敛域
二、 幂级数及收敛域 定理 2 设幂级数 0 n n n a x 的系数满足 lim | | 1 n n n a a 则这幂级数的收敛半径 0 0 1 0 R 例 2 求幂级数 0 ! n n x n 的收敛半径和收敛域 第一步:确定幂级数 0 n n n a x 的系数通项 n a 第二步:计算极限 lim | | 1 n n n a a 第三步:确定 0 n n n a x 的收敛半径 第四步:确定 0 n n n a x 的收敛域 解 显然 1 ! n a n . 因此 1 1 ( 1)! 1 lim | | lim lim 0 1 1 ! n n n n n a n a n n 所以 0,故收敛半径为 R 因此幂级数 0 ! n n x n 的收敛域为 ( , ).