
§10.1常数项级数的概念及性质 常数项级数概念 无穷级数性质 级数收敛的条件 应 用
§10.1 常数项级数的概念及性质 常数项级数概念 无穷 级数性质 级数 收敛的条件 应 用

回顾数列的性质 数列: 141,42,…,n,… 前n项和: Sn=4+山2+43,+…十un lim s=s n-→0 单调有界数列必收敛 若一数列收敛于5,则其任意的子列必收敛于s 若limS2n=S,limS2m1=S 若limS2n=S,limS2m1=S2,且 n→0 n-y0 1300 则 lims=s S1≠S2 则数列3,必发散 1→00
背景:求曲顶柱体的体积 一、 回顾数列的性质 数列: 1 2 , , , , n u u u 前 n 项和: 1 2 3, n n s u u u u 单调有界数列必收敛 若一数列收敛于s, 则其任意的子列必收敛于s 若 2 2 1 lim ,lim n n n n s s s s 若 2 1 2 1 2 lim ,lim n n n n s s s s ,且 1 2 s s 则数列 n s 必发散 lim n n s s 则 lim n n s s
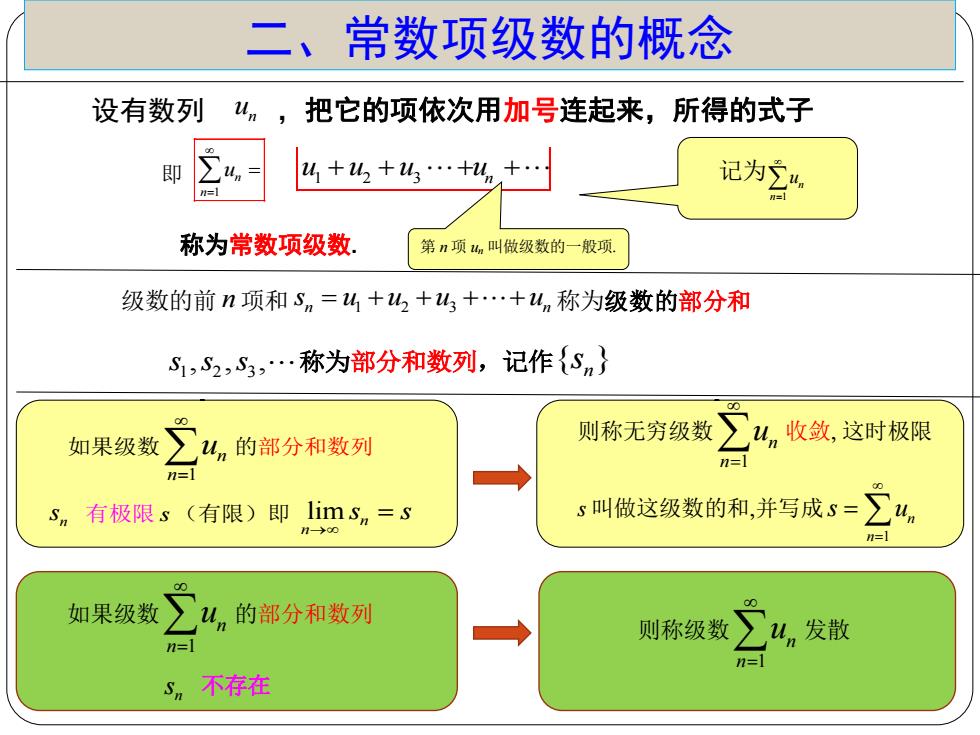
二、常数项级数的概念 设有数列 4,,把它的项依次用加号连起来,所得的式子 即 un 41+42+%3…+,+ 记为吃4 称为常数项级数. 第n项n叫做级数的一般项 级数的前n项和Sn=4+山2+43+…+山n称为级数的部分和 S,52,S,…称为部分和数列,记作{Sn} 00 如果级数 山,的部分和数列 则称无穷级数 4n收敛,这时极限 n=] n= Sn 有极限s(有限)即lim s=s n→0 ,叫做这级数的和,并写成5=∑4 n=l 如果级数 u.的部分和数列 则称级数 n=l ∑,发散 2= Sn不存在
二、常数项级数的概念 设有数列 n u ,把它的项依次用加号连起来,所得的式子 1 2 3 n u u u u 称为常数项级数. 即 1 n n u 记为 n1 n u 级数的前 n 项和 n n 1 2 3 s u u u u 称为级数的部分和 第 n 项 un 叫做级数的一般项 1 2 3 s s s , , , 称为部分和数列,记作{ }n s 如果级数 n1 un 的部分和数列 n s 有极限 s (有限)即 lim n n s s 如果级数 n1 n u 的部分和数列 n s 不存在 则称无穷级数 n1 un 收敛 这时极限 s 叫做这级数的和并写成 1 n n s u 则称级数 n1 n u 发散

二、常数项级数的概念 当级数了 收敛时,其部分和sn是级数 的和s的近似值它们之间的差值 00 'n=S一Sn=4n+1+4n+2十…叫做级数 un的余项。 n=1 注记1: 级数u 收敛的充要条件是其部分和数列、收敛 n=1 级数】 发散的充要条件是其部分和s,数列发散 注记2:级数 ,收敛的充要条件是m。=s,lm=S 10 n=1 注记3:用定义判断级数 收敛的一般步骤 n=1 第一步:计算 的前n项和Sn;第二步:判断Sn是否收敛 n=
二、常数项级数的概念 当级数 n1 un 收敛时 其部分和 n s 是级数 n1 un 的和s 的近似值 它们之间的差值 n n n n 1 2 r s s u u 叫做级数 n1 un 的余项 注记 1:级数 n1 n u 收敛的充要条件是其部分和数列 n s 收敛 级数 n1 un 发散的充要条件是其部分和 n s 数列发散 注记 2:级数 n1 n u 收敛的充要条件是 2 2 1 lim ,lim n n n n s s s s 注记 3:用定义判断级数 n1 n u 收敛的一般步骤 第一步:计算 n1 n u 的前n 项和 n s ;第二步:判断 n s 是否收敛
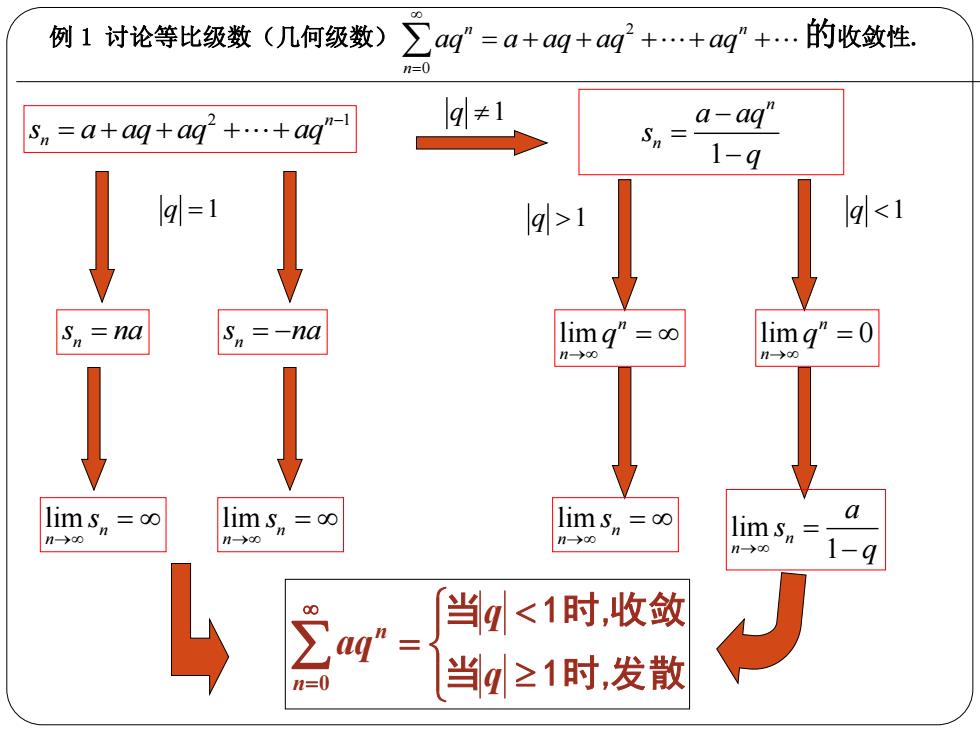
例1讨论等比级数(几何级数) ∑ag=a+ag+ag2+…+ag+…的收敛性. n= sn=a+aq+ag+…+ag" lql≠1 a-aq" Sn= 1-q g=1 q>1 14l<1 S,=na S,=-na limg”=o∞ limg"=0 n-→c0 1-→0 lims,=o lims,=o lims,=o a 1-→c0 1→o0 1-→c0 lims,= 1-→00 1-9 q"= 当q<1时,收敛 1=0 当 ≥1时,发散
例 1 讨论等比级数(几何级数) 2 0 n n n aq a aq aq aq 的收敛性. 2 1 n n s a aq aq aq q 1 1 n n a aq s q q 1 n s na lim n n s n s na lim n n s q 1 lim n n q lim n n s q 1 lim 0 n n q lim 1 n n a s q 当 1时,发散 当 1时,收敛 q q aq n n 0