
·10· 第1章n阶行列式 故所给的项在六阶行列式的展开式中应带正号. 例8确定 2x -x 1 2 -1 x 1 -1 f(x)= 2 1 -5x-1 1 -123x 中x与x2的系数 解由于只有对角线的元素相乘才出现x,而且这一项带正号,即 a1a2aa44=2x·x·(-5x)·3x=-30x.故f(x)中x的系数为-30. 同理含x的项也只有一项,即 a12a1aaaa4=(-x)·(-1)·(-5x)·3x=-15x2. 而列标所构成的排列的逆序数 x(2134)=1+0+0=1, 故f(x)中含x3的项为15x2,系数为15. 由定理1.1.1可知,三阶行列式 anan ai a21a2a23 asas ass =∑(-1)rNa1nana% A为P内 =ananan +ananas +ananas-ansazan-anazan-andnass. 定理1.11虽然给出了n阶行列式的完全表达式,但在具体应用定理解决问 题时比较困难。 1.2n阶行列式的性质 利用行列式的定义计算特殊类型的行列式比较简单,但对一般的行列式,特别 是高阶行列式,计算量相当大.为简化行列式的计算,下面我们来讨论行列式的性 质.首先介绍一个重要的定理, 由上节n阶行列式的定义(1.9)式可知,n阶行列式可表示为第一行的元素与 其对应的代数余子式的乘积之和,因此,(1.9)式又称为行列式按第一行的展开 式,事实上,行列式可按任意一行(列)展开 定理1.2.1n阶行列式等于它的任意一行(列)的各元素与其对应的代数余 子式的乘积之和,即 D=a1A1+a2A2+.+anAn(i=1,2,.,n)

1.2n阶行列式的性质 ·11· 或 D=aA十a2Agy+.十awAw(j=1,2,.,n). 证明略. 推论如果n阶行列式中第i行所有元素除ag外都为零,那么行列式就等于 ag与其对应的代数余子式的乘积,即 D=aA. 设n阶行列式 ala2.a1n D= aal an.am 若把D中每一行元素换成同序数的列元素,则得新行列式 a1a21.aml D= aza.an2 ama2n.am 称D(或记为D)为行列式D的转置行列式. 性质1.2.1行列式与它的转置行列式相等 证用数学归纳法. 当-■论立 假设对n一1阶行列式结论成立,对于n阶行列式D和D',分别按第一行和第 一列展开,得 D=2a-1DM=之a,(-1D a.dny-i dam.an a21 .aa .a .g 由于M,和M:,是n一1阶行列式,且M,是M,的转置行列式,根据假设M,= M',于是D=D

·12· 第1章n阶行列式 例如,上三角行列式 a1la12.a1m D= 0a2.a2 0 0.am 由定理1.2.1的推论即得 a0.0 D=D'= .0 =a11Q22*am alm azn.a 性质1.2.1表明,行列式中行与列具有同等的地位,行列式的性质凡是对行成 立的对列也同样成立,反之亦然。 性质1.2.2互换行列式两行(列)的元素,行列式变号。 证 用数学归纳法. 当n=2时,aae aa,结论成立. 假设对于n一1阶行列式结论成立,对于n阶行列式 a11a12.a1m anaea D= aae.an 互换D中的第s行和第I行,得 aae.an D1=:: anaa anan.an 分别将D和D1按第i行展开(i≠s,),得 D=2a,←M,=2a,(-DN

1,2n阶行列式的性质 ·13· 其中M,和N。分别为D和D,中元素a。的余子式,并且N,是由M,互换两行得 到的n一1阶行列式,由归纳假设M,=一N,因此D=一D. 通常以,表示行列式的第i行,以,表示行列式第i列,交换i,)两行记作 r,+r,而交换i,j两列记作c,c: 推论行列式中有两行(列)对应元素相等,行列式的值为零 证互换行列式D中对应元素相等的两行,则D=一D,故D=0, 性质1,2.3行列式中某一行(列)的所有元素都乘以同一数k,等于用数k乘 此行列式,即 an a2. a4ai2.an haa kae.an=为aa.an a.a alae.a 证将左边行列式按第行展开即得。 第i行(列)乘以,记作:,(c). 推论1行列式中某一行(列)的所有元素的公因子可以提到行列式符号 外面 推论2若行列式中有一行(列)的元素全为零,则行列式为零 推论3若行列式中有两行(列)对应元素成比例,则行列式为零 性质1.2.4若行列式中某一行(列)的元素a,都可分解为两元素b。与c。之 和,即a,=bu十cw(j=1,2,.,n,1≤i≤n),则该行列式可分解为相应的两个 行列式之和,即 an a12 din D=ba+cab2十ca.bn十c a11a12 .a1aia =bba.b ca ca c anla2am an a,.am 证将D按第i行展开: D=∑6,+e)A=bA+ cA。=D+D2, e1 =1 =1
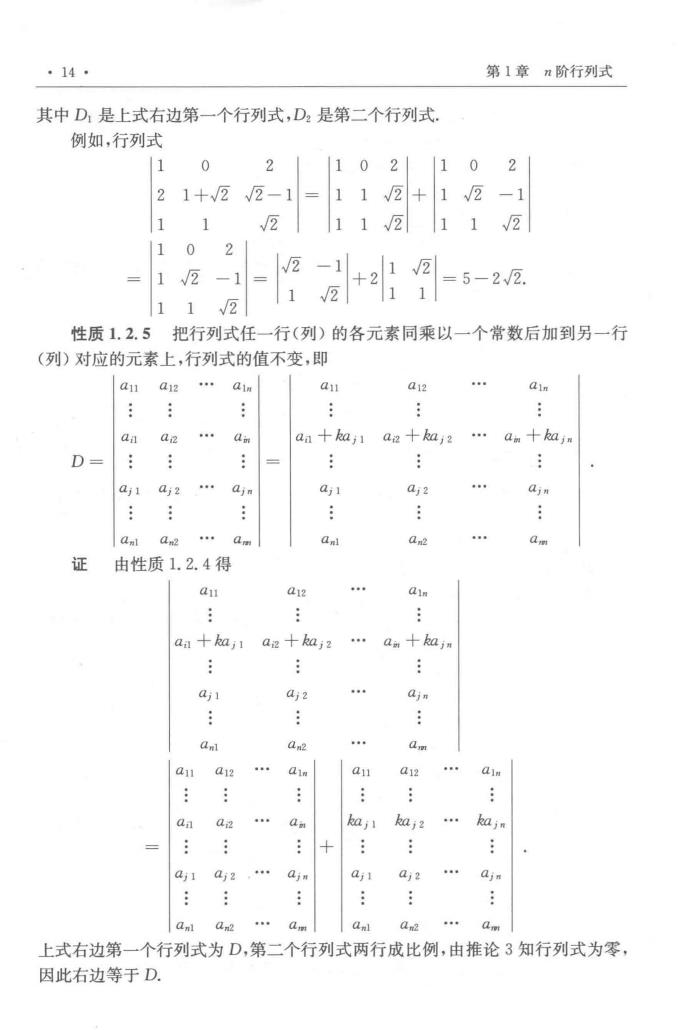
·14 第1章n阶行列式 其中D是上式右边第一个行列式,D2是第二个行列式, 例如,行列式 11 0 2 1102102 21+√2√2-1=11√2+1√2-1 1 1 2112112 1102 =12-1= 2-1 +2 =5-2√2 112 1√2 11 性质1.2.5把行列式任一行(列)的各元素同乘以一个常数后加到另一行 (列)对应的元素上,行列式的值不变,即 a1a12a1m an a12 aa十aj1a2十ka,2 .a十ba D= = . a 由性质1.2.4得 aa十a,1 aa十k如j2.am十kaj ajl aj2 ajn a11a12 an a12 aj? aj? ajn a 上式右边第一个行列式为D,第二个行列式两行成比例,由推论3知行列式为零, 因此右边等于D