
概率论与散理统外「 (2)分布函数的性质 1°F(x,y)是变量x和y的不减函数,即对于任 意固定的y,当x2>x1时F(2y)≥F(x1,y) 对于任意固定的c,当y2>y时F(x,2)≥F(x,y1) 2°0≤F(x,y)≤1,且有 对于任意固定的y,F(-oo,y)=imF(x,y)=0, 〉-0 对于任意固定的x,F(x,-oo)=limF(x,y)=0, F(-00,-00)=lim F(x,y)=0, y→-0
(2) 分布函数的性质 , ( , ) ( , ), 1 ( , ) , 2 1 2 1 o y x x F x y F x y F x y x y 意固定的 当 时 是变量 和 的不减函数 即对于任 , ( , ) ( , ). 2 1 2 1 对于任意固定的x 当y y时F x y F x y 2 0 ( , ) 1, o F x y 对于任意固定的y, (, ) lim ( , ) 0, F y F x y x 且有 对于任意固定的x, ( ,) lim ( , ) 0, F x F x y y (,) lim ( , ) 0, F F x y y x
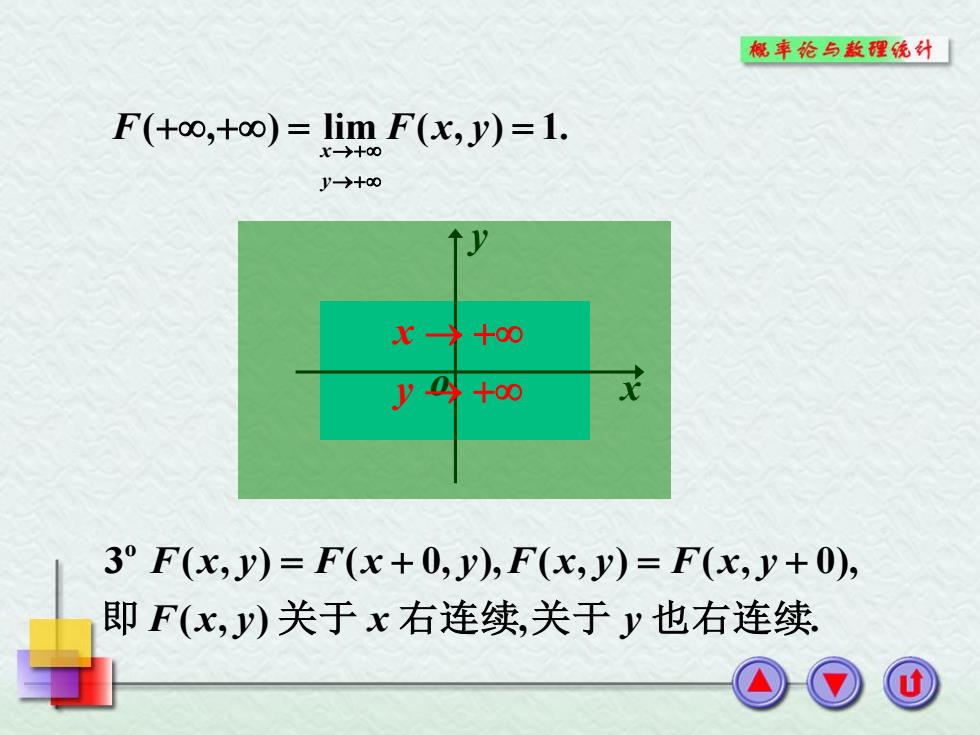
概率论与敖理统计 F(+o0,+oo)=lim F(x,y)=1. y-→+0 +00 3°F(x,y)=F(x+0,y),F(,y)=F(x,y+0), 即F(x,y)关于x右连续,关于y也右连续
(,) lim ( , ) 1. F F x y y x ( , ) , . 3 ( , ) ( 0, ), ( , ) ( , 0), o 即 F x y 关 于 x 右连续 关 于 y 也右连续 F x y F x y F x y F x y o x y y x

概率伦与教理统针」 4对于任意(x1,y1),(x2,y2),X1<x2,y1<y2 有F(x2,Jy2)-F(x21)+F(K1,1)-F(x1,y2)≥0. 证明P{x,<X≤x2,1<Y≤y2} =P{X≤x2,1<Y≤y2}P{X≤x1,1<Y≤y2} =P{X≤x2,Y≤y2}-P{X≤x2,Y≤y} -P{X≤x1,Y≤y2}+P{X≤x1,Y≤y1}≥0, 故F(x2,y2)-F(x2,y)+F(x1,y1)-F(x1,2)≥0
4 ( , ),( , ), , , 1 1 2 2 1 2 1 2 o 对于任意 x y x y x x y y ( , ) ( , ) ( , ) ( , ) 0. 有 F x2 y2 F x2 y1 F x1 y1 F x1 y2 证明 { , } 1 2 1 2 P x X x y Y y 0, { , } 2 1 2 P X x y Y y { , } 2 2 P X x Y y ( , ) ( , ) ( , ) ( , ) 0. 故 F x2 y2 F x2 y1 F x1 y1 F x1 y2 { , } 1 1 2 P X x y Y y { , } 2 1 P X x Y y { , } 1 2 P X x Y y { , } 1 1 P X x Y y

概率论与敖理统外 二、二维离散型随机变量 1.定义 若二维随机变量(X,Y)所取的可能值是有 限对或无限可列多对,则称(X,Y)为二维离散型 随机变量
若二维随机变量 ( X, Y ) 所取的可能值是有 限对或无限可列多对,则称 ( X, Y ) 为二维离散型 随机变量. 二、二维离散型随机变量 1. 定义

概率论与数理统外「 2.二维离散型随机变量的分布律 设二维离散型随机变量(X,Y)所有可能取的 值为(x,y),i,j=1,2,.,记 p{X=xi,Y=yi}=pi,i,j=1,2,., 称此为二维离散型随机变量(X,Y)的分布律,或 随机变量X和Y的联合分布律. 其中p,≥0,∑∑P,=1. i=1j=1
2. 二维离散型随机变量的分布律 ( , ) ( , ), , 1,2, , { , } , , 1,2, , ( , ) , . i j i j ij X Y x y i j P X x Y y p i j X Y X Y 设二维离散型随机变量 所有可能取的 值为 记 称此为二维离散型随机变量 的分布律 或 随机变量 和 的联合分布律 0, 1. 1 1 i j ij ij 其 中 p p