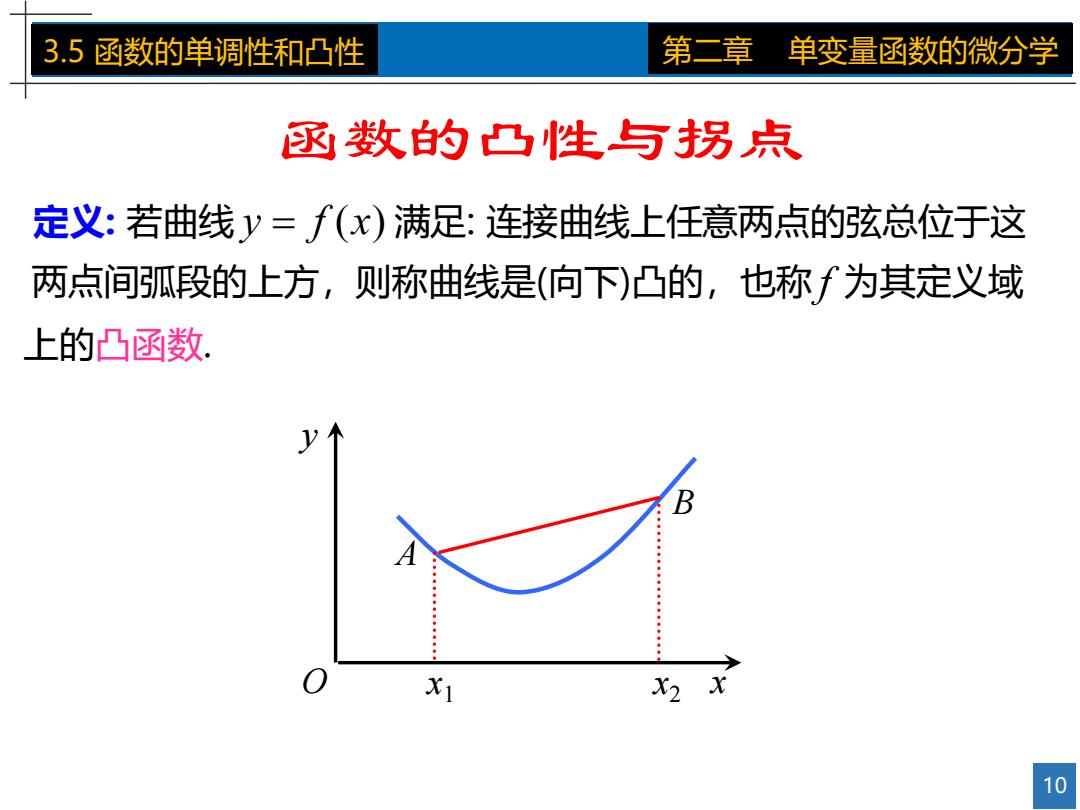
3.5函数的单调性和凸性 第二章 单变量函数的微分学 诬数的凸性与拐点 定义:若曲线y=f(x)满足:连接曲线上任意两点的弦总位于这 两点间弧段的上方,则称曲线是(向下)凸的,也称f为其定义域 上的凸函数. B A X1 X2 X 10
10 3.5 函数的单调性和凸性 第二章 单变量函数的微分学 函数的凸性与拐点 定义: 若曲线 满足: 连接曲线上任意两点的弦总位于这 两点间弧段的上方,则称曲线是(向下)凸的,也称 为其定义域 上的凸函数. O x y A B x1 x2
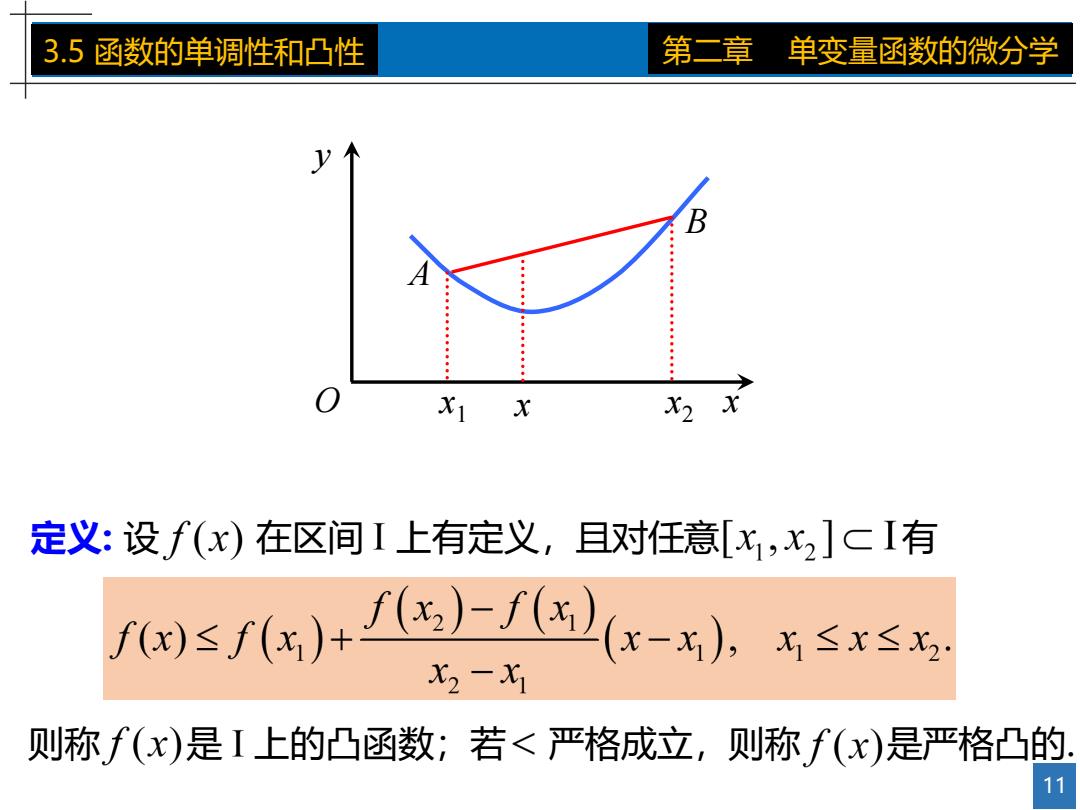
3.5函数的单调性和凸性 第二章 单变量函数的微分学 X2 定义:设f(x)在区间I上有定义,且对任意[x,x,]CI有 ))+)f(). X2-X 则称f(x)是I上的凸函数;若<严格成立,则称f(x)是严格凸的 11
11 3.5 函数的单调性和凸性 第二章 单变量函数的微分学 O x y A B x1 x x2 定义: 设 在区间 上有定义,且对任意 有 则称 是 上的凸函数;若 严格成立,则称 是严格凸的

3.5函数的单调性和凸性 第二章 单变量函数的微分学 定义:设f(x)在区间I上有定义,且对任意[x,x2]CI有 ≤f)+西)-f(x-x,xsx≤ X2-X1 则称f(x)是I上的凸函数,或f(x)在I上凸. 令x=ax1+(1-)x,(a∈(0,1),可得: 定理:f(x)在区间I上凸台[x,x2]cL,∈(0,1) f(ax+(1-a)x2)≤af(x)+(1-)f(x2). 定理:f(x)在区间I上连续.则f(x)凸台[x,x2]CI, f(x)+f(x2) 2 2 12
12 3.5 函数的单调性和凸性 第二章 单变量函数的微分学 令 可得: 定理: 在区间 上凸 定理: 在区间 上连续. 则 凸 定义: 设 在区间 上有定义,且对任意 有 则称 是 上的凸函数,或 在 上凸