
3、配置积分限,化二重积分为二次积分并作定积分计算122N2y=-vi-x2V = 6] dg - 3]] x?dg - 3]] y?dgDDDJJ d = 2元而DI[ xdo=ydoDD由x,V的对称性有/2x2/2V2J x?do=了x2dx[dy=2 [ x?~2-d-V22DV2-x2"V22-x?dx=4f4sin?0cos?0V2=41x00= 16. (2 -1)(2 -1)!!元2(2 + 2)!!1.1 元= 16.4.22=元所求立体的体积为V=12元-6元=6元例5、求两个底圆半径为R且这两个圆柱面的方程分别为x2+y2=R2及x?+=?=R2.求所围成的立体的体积。解:
3、配置积分限, 化二重积分为二次积分并作定积分计算 V d xd yd DD D =− − 63 3 ∫∫ ∫∫ ∫∫ 2 2 σσσ 而 d D ∫∫ σ = 2π 由 x , y 的对称性有 xd yd D D 2 2 ∫∫ ∫∫ σ σ = x d x dx dy x x dx D x x 2 2 2 2 2 2 2 2 2 2 2 2 ∫∫ ∫ ∫ ∫ σ = =− 2 2 − − − − − = −= 4 2 44 ∫ ∫ 2 2 0 2 2 2 0 2 x x dx sin cos θ θ π = ⋅ − − + 16 ⋅ 21 21 22 2 ( )!!( )!! ( )!! π = ⋅ ⋅ ⋅ 16 ⋅ 1 1 42 2 π = π 所求立体的体积为 V = −= 12 6 6 π π π 例 5、求两个底圆半径为 R, 且这两个圆柱面的方程分别为 22 2 x + = y R 及 22 2 x + = z R .求所围成的立体的体积。 解:
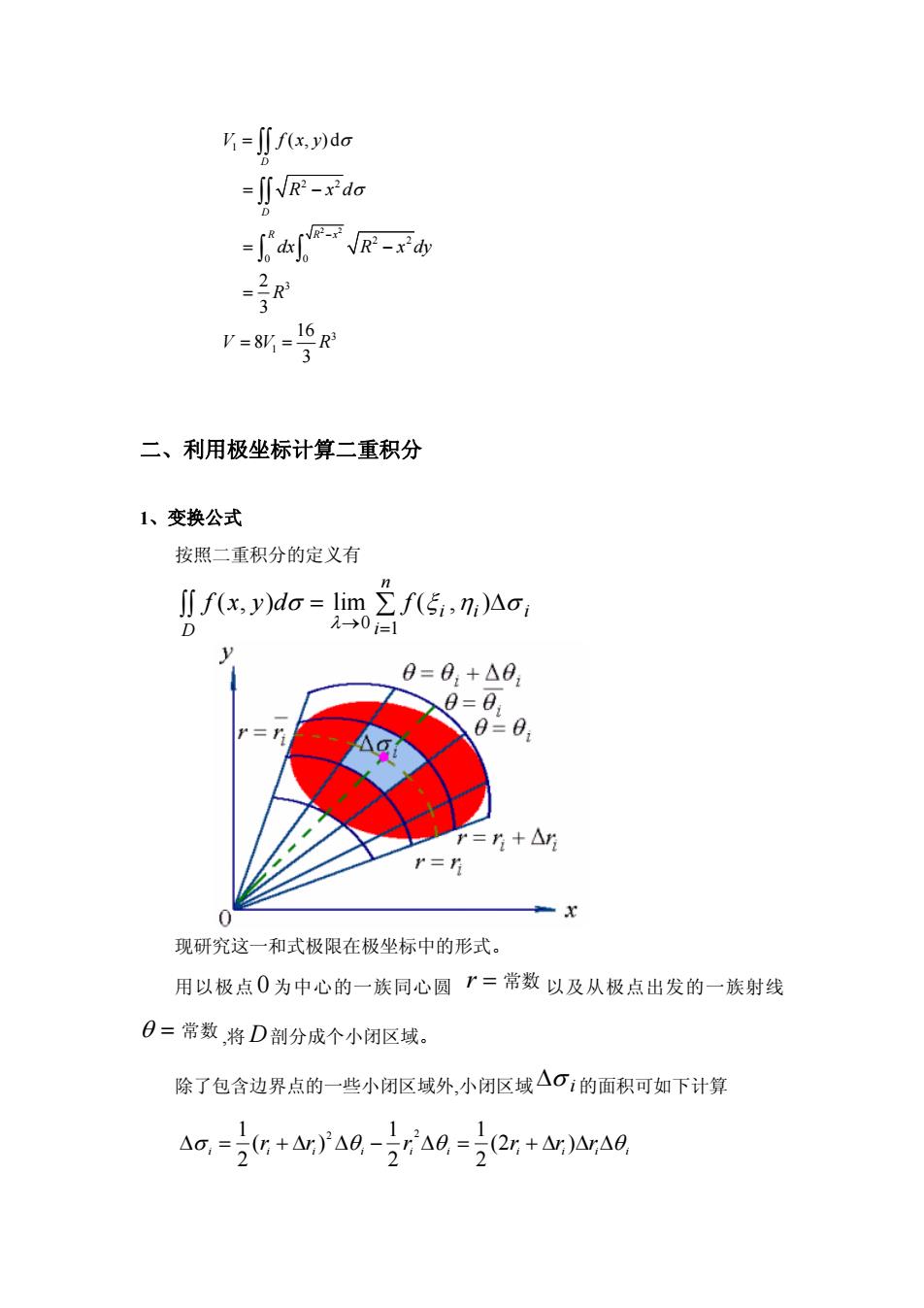
(x,y)doIR-dgR?-xdy2R3316RV = 8V =3二、利用极坐标计算二重积分1、变换公式按照二重积分的定义有J[ f(x, y)do = lim Z f(5i,n,)Ao入→0=1O/6=0,+20,0=00=0r=r +Arr=rX0现研究这一和式极限在极坐标中的形式。用以极点O为中心的一族同心圆r=常数以及从极点出发的一族射线O=常数,将D剖分成个小闭区域。除了包含边界点的一些小闭区域外,小闭区域△i的面积可如下计算rsa=!(r +Nr)e (2r+r)ArA0Ao,:
2 2 1 2 2 2 2 0 0 3 3 1 ( , )d 2 3 16 8 3 D D R Rx V f xy R xd dx R x dy R VV R σ σ − = = − = − = = = ∫∫ ∫∫ ∫ ∫ 二、利用极坐标计算二重积分 1、变换公式 按照二重积分的定义有 f xyd f D ii i i n ( , ) lim ( , ) σ ξη σ λ ∫∫ = ∑ → = 0 1 Δ 现研究这一和式极限在极坐标中的形式。 用以极点 0 为中心的一族同心圆 r = 常数 以及从极点出发的一族射线 θ = 常数 ,将 D剖分成个小闭区域。 除了包含边界点的一些小闭区域外,小闭区域Δσ i 的面积可如下计算 i i i i i i i i i i Δσ = r + Δr Δθ − r Δθ = (2r + Δr)ΔrΔθ 2 1 2 1 ( ) 2 1 2 2