
第八章多元函数微分法及其应用第一节:多元函数的基本概念教学目的:学习并掌握关于多元函数的区域、极限以及多元函数概念,掌握多元函数的连续性定理,能够判断多元函数的连续性,能够求出连续函数在连续点的极限。教学重点:多元函数概念和极限,多元函数的连续性定理。教学难点:计算多元函数的极限。教学内容:第一节多元函数的基本概念一区域讨论一元函数时,经常用到邻域和区间的概念。由于讨论多元函数的需要,我们首先把邻域和区间概念加以推广,同时还要涉及其它一些概念。1.邻域设p(xo,yo)是xoy平面上的一个点,是某一正数。与点P。(xoyo)距离小于的点p(x,y)的全体,称为点P。的邻域,记为U(Po,),即U(Po,0)=(PPP/ <8) ,也就是U(Po,8)=((x, ) 1 /(x-xo)~ +(y- yo)2 <8)。在几何上,U(Po,)就是xoy平面以上点p(xo,y)为中心、>0为半径的圆的内部的点P(x,y)的全体。2.区域设E是平面上的一个点集,P是平面上的一个点。如果存在点P的某一邻域U(P)CE,则称P为E的内点(画图8-1显示)。显然,E的内点属于E
第 八 章 多元函数微分法及其应用 第 一 节:多元函数的基本概念 教学目的:学习并掌握关于多元函数的区域、极限以及多元函数概念,掌握多元 函数的连续性定理,能够判断多元函数的连续性,能够求出连续函数 在连续点的极限。 教学重点:多元函数概念和极限,多元函数的连续性定理。 教学难点:计算多元函数的极限。 教学内容: 第一节 多元函数的基本概念 一、 区 域 讨论一元函数时,经常用到邻域和区间的概念。由于讨论多元函数的需要,我们首先 把邻域和区间概念加以推广,同时还要涉及其它一些概念。 1. 邻域 设 ( , ) 0 0 0 p x y 是 xoy 平面上的一个点,δ 是某一正数。与点 ( , ) 0 0 0 p x y 距离小于δ 的 点 p(, ) x y 的全体,称为点 P0 的δ 邻域,记为 ( , ) U P0 δ ,即 ( , ) U P0 δ ={ } P PP0 < δ , 也就是 ( , ) U P0 δ = { (x, y)│ − + − < δ 2 0 2 0 (x x ) ( y y ) }。 在几何上, ( , ) U P0 δ 就是 xoy 平面以上点 ( , ) 0 0 0 p x y 为中心、δ > 0 为半径的圆的内 部的点 P(x, y) 的全体。 2. 区域 设 E 是平面上的一个点集,P 是平面上的一个点。如果存在点 P 的某一邻域U(P) ⊂ E , 则称 P 为 E 的内点(画图 8-1 显示)。显然, E 的内点属于 E

如果E的点都是内点,则称E为开集。例如,点集E,=((x,y)<x2+y2<4)中每个点都是E,的内点,因此E,为开集。如果点P的任一邻域内既有属于E的点,也有不属于E的点(点P本身可以属于E,也可以不属于E),则称P为E的边界点(可画图8-2显示)。E的边界点的全体称为E的边界。例如上例中,E的边界是圆周x+y?=1和x+y=4。设D是开集。如果对于D内任何两点,都可用折线连结起来,且该折线上的点都属于D,则称开集D是连通的。连通的开集称为区域或开区域。例如,((x,)x+>0)及(x,y)l<x2+y24)都是区域。开区域连同它的边界一起,称为闭区域,例如((x,y) /x+y≥0)及((x,y) /1≤x2+y≤4)都是闭区域。对于点集E,如果存在正数K,使一切点PEE与某一定点A间的距离IAP不超过K,即AP≤k,对一切PEE成立则称E为有界点集,否则称为无界点集。例如,((x,y)11≤x2+y2≤4)是有界闭区域,((x,y)Ix+y>0)是无界开区域。3.n维空间我们知道,数轴上的点与实数有一一对应关系,从而实数全体表示数轴上一切点的集合,即直线。在平面上引入直角坐标系后,平面上的点与二元数组(x,y)一一对应,从而二元数组(xy)全体表示平面上一切点的集合,即平面。在空间引入直角坐标系后,空间的点与三元数组(xy,z)一一对应,从而三元数组(x,y,=)全体表示空间一切点的集合,即空间。一般地,设n为取定的一个自然数,我们称n元数组(x,r2,",x,)的全体为n维空间,而每个n元数组(x,x2,",x,)称为n维空间中的一个点,数x称为该点的第i个坐标。n维空间记为R"。n维空间中两点P(x,X2",x)及Q(x,X2,",x)间的距离规定为
如果 E 的点都是内点,则称 E 为开集。例如,点集 {( , )1 4} 2 2 E1 = x y < x + y < 中每 个点都是 E 1 的内点,因此 E 1为开集。 如果点 P 的任一邻域内既有属于 E 的点,也有不属于 E 的点(点 P 本身可以属于 E , 也可以不属于 E ),则称 P 为 E 的边界点(可画图 8-2 显示)。E 的边界点的全体称为 E 的 边界。例如上例中, E 1 的边界是圆周 1 2 2 x + y = 和 2 2 x + y =4。 设 D 是开集。如果对于 D 内任何两点,都可用折线连结起来,且该折线上的点都属于 D,则称开集 D 是连通的。 连通的开集称为区域或开区域。例如,{(x, y) x + y > 0}及{( , )1 4} 2 2 x y < x + y < 都 是区域。 开区域连同它的边界一起,称为闭区域,例如 { (x, y)│ x + y ≥0}及{ (x, y)│1≤ 2 2 x + y ≤4} 都是闭区域。 对于点集 E ,如果存在正数 K,使一切点 P ∈ E 与某一定点 A 间的距离|A P |不超过 K, 即 |A P |≤k, 对一切 P ∈ E 成立, 则称 E 为有界点集,否则称为无界点集。例如,{ (x, y)│1≤ 2 2 x + y ≤4}是有界闭区域, { (x, y)│ x + y >0}是无界开区域。 3. n 维空间 我们知道,数轴上的点与实数有一一对应关系,从而实数全体表示数轴上一切点的集合, 即直线。在平面上引入直角坐标系后,平面上的点与二元数组(x, y)一一对应,从而二元数 组(x, y)全体表示平面上一切点的集合,即平面。在空间引入直角坐标系后,空间的点与三 元数组( x, y,z )一一对应,从而三元数组( x, y,z )全体表示空间一切点的集合,即空间。 一般地,设 n 为取定的一个自然数,我们称n 元数组( n x , x , , x 1 2 " )的全体为 n 维空间, 而每个 n 元数组( , , , ) 1 2 n x x " x 称为 n 维空间中的一个点,数 xi 称为该点的第 i 个坐标。n 维 空间记为 Rn 。 n 维空间中两点 ( , , , ) 1 2 n P x x " x 及 ( , , , ) 1 2 n Q x x " x 间的距离规定为

[Pg| = /(y -x,)2 +(y2 -x,)2 +...+(y, -x,)。容易验知,当n=1,2,3时,由上式便得解析几何中关于直线(数轴),平面,空间内两点的距离。前面就平面点集来陈述的一系列概念,可推广到n维空间中去。例如,设P。ER”,是某一正数,则n维空间内的点集U(Po,0)=(PPP<8,PER")就定义为点P。的邻域。以邻域概念为基础,可定义内点、边界点、区域、聚点等一系列概念。二、多元函数概念在很多自然现象以及实际问题中,经常遇到多个变量之间的依赖关系,举例如下:例1圆柱体的体积V和它的底半径r、高h之间具有关系V=mr*h。这里,当r、h在集合(r,h)r>0,h>0)内取定一对值(r,h)时,V的对应值就随之确定。例2一定量的理想气体的压强P、体积V和绝对温度T之间具有关系RTp=V'其中R为常数。这里,当V、T在集合(V,T)V>0,T>O)时,p的对应值就随之确定。例3设R是电阻R、R并联后的总电阻,由电学知道,它们之间具有关系R,R,R=-R, + R2对应值就随之确定。上面三个例子的具体意义虽各不相同,但它们却有共同的性质,抽象出这些共性就可得出以下二元函数的定义。定义一设D是平面上的一个点集。如果对于每个点P(x,Jy)eD,变量z按照一定法则总有确定的值和它对应,则称z是变量x、y的二元函数(或点P的函数),记为z= f(x,y) (或z=f(P))
2 2 2 2 2 1 1 ( ) ( ) ( ) n n PQ = y − x + y − x +"+ y − x 。 容易验知,当 n =1,2,3 时,由上式便得解析几何中关于直线(数轴),平面,空间内两点 的距离。 前面就平面点集来陈述的一系列概念,可推广到 n 维空间中去。例如,设 n P0 ∈ R ,δ 是某一正数,则 n 维空间内的点集 ( , ) U P0 δ ={ , } 0 n P PP < δ P ∈ R 就定义为点 P0 的δ 邻域。以邻域概念为基础,可定义内点、边界点、区域、聚点等一系列 概念。 二、多元函数概念 在很多自然现象以及实际问题中,经常遇到多个变量之间的依赖关系,举例如下: 例 1 圆柱体的体积 V 和它的底半径 r 、高 h 之间具有关系 V r h 2 = π 。 这里,当 r 、h 在集合{(r,h)r > 0, h > 0}内取定一对值(r,h) 时,V 的对应值就随之确定。 例 2 一定量的理想气体的压强 p 、体积V 和绝对温度T 之间具有关系 p = V RT , 其中 R 为常数。这里,当V 、T 在集合{(V,T)V > 0,T > 0}时, p 的对应值就随之确定。 例 3 设 R 是电阻 R1、 R2 并联后的总电阻,由电学知道,它们之间具有关系 1 2 1 2 R R R R R + = 对应值就随之确定。 上面三个例子的具体意义虽各不相同,但它们却有共同的性质,抽象出这些共性就可 得出以下二元函数的定义。 定义一 设 D 是平面上的一个点集。如果对于每个点 P(x, y) ∈ D ,变量 z 按照一定法 则总有确定的值和它对应,则称 z 是变量 x、y 的二元函数(或点 P 的函数),记为 z = f (x, y) (或 z = f (P) )

点集D称为该函数的定义域,X、y称为自变量,z也称为因变量。数集(=z = f(x,y),(x,y)e D)称为该函数的值域。z是x,y的函数也可记为z=z(x,y),z=Φ(x,y)等等。类似地可以定义三元函数u=f(x,J,=)以及三元以上的函数。一般的,把定义1中的平面点集D换成n维空间内的点集D,则可类似地可以定义n元函数u=f(x,x2,",x)。n元函数也可简记为u=f(P),这里点P(x,x2,"",x)eD。当n=1时,n元函数就是一元函数。当n≥2时,n元函数就统称为多元函数。关于多元函数定义域,与一元函数类似,我们作如下约定:在一般地讨论用算式表达的多元函数u=f(P)时,就以使这个算式有确定值u的自变量所确定的点集为这个函数的定义域。例3,求下列函数的定义域1. z= ln(x+y)解:函数z=ln(x+y)的定义域为((x+y)x+y>0)(图8-3),就是一个无界开区域。2. z=arcsin(x2 +y)解:函数z=arcsin(x2+y)的定义域为(x+ y)x? + y? ≤1)(图8-4),这是一个闭区域。x+y=0
点集 D 称为该函数的定义域, x、y 称为自变量, z 也称为因变量。数集 {z z = f (x, y),(x, y) ∈ D} 称为该函数的值域。 z 是 x, y 的函数也可记为 z = z(x, y) , z = Φ(x, y)等等。 类似地可以定义三元函数u = f (x, y,z) 以及三元以上的函数。一般的,把定义 1 中的 平面点集 D 换 成 n 维空间内的点集 D ,则可类似地可以定义 n 元函数 ( , , , ) 1 2 n u = f x x " x 。 n 元函数也可简记为u = f (P) ,这里点 P(x1 , x2 ,", xn ) ∈ D 。当 n = 1时, n 元函数就是一元函数。当 n ≥ 2时,n 元函数就统称为多元函数。 关于多元函数定义域,与一元函数类似,我们作如下约定:在一般地讨论用算式表达 的多元函数u = f (P) 时,就以使这个算式有确定值 u 的自变量所确定的点集为这个函数的 定义域。 例 3,求下列函数的定义域 1. z = ln(x + y) 解 :函数 z = ln(x + y)的定义域为 {(x + y) x + y > 0} (图 8-3),就是一个无界开区域。 2. arcsin( ) 2 2 z = x + y 解 :函数 arcsin( ) 2 2 z = x + y 的定义域为 {( ) 1} 2 2 x + y x + y ≤ (图 8-4),这是一个闭区域。 x+y=0
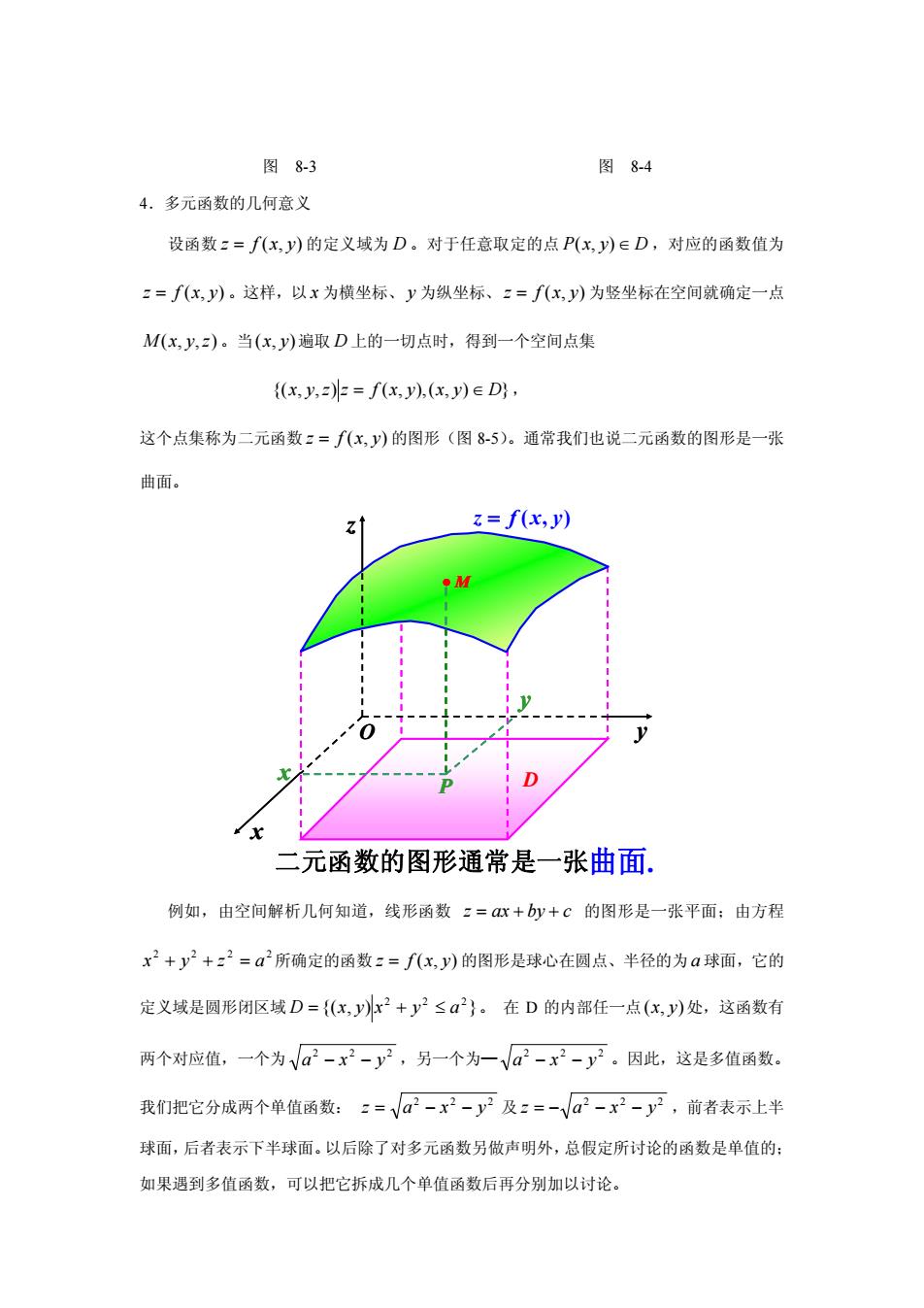
图8-4图8-34.多元函数的几何意义设函数z=f(x,y)的定义域为D。对于任意取定的点 P(x,y)eD,对应的函数值为z=f(x,y)。这样,以x为横坐标、为纵坐标、z=f(x,y)为竖坐标在空间就确定一点M(x,y,z)。当(x,y)遍取D上的一切点时,得到一个空间点集((x,y,=)z= f(x,y),(x,y)e D) ,这个点集称为二元函数z=f(x,y)的图形(图8-5)。通常我们也说二元函数的图形是一张曲面。z = f(x,y)Z2y二元函数的图形通常是一张曲面例如,由空间解析几何知道,线形函数z=ax+by+c的图形是一张平面;由方程x2+y?+=2=α所确定的函数z=f(x,J)的图形是球心在圆点、半径的为α球面,它的定义域是圆形闭区域D=(x,J)x2+y2≤α2)。在D的内部任一点(x,J)处,这函数有两个对应值,一个为a2-x2-y2,另一个为一a2-x2-y2。因此,这是多值函数。我们把它分成两个单值函数:z=a2-x?-y2及z=-a2-x-y,前者表示上半球面,后者表示下半球面。以后除了对多元函数另做声明外,总假定所讨论的函数是单值的;如果遇到多值函数,可以把它拆成几个单值函数后再分别加以讨论
4.多元函数的几何意义 设函数 z = f (x, y) 的定义域为 D 。对于任意取定的点 P(x, y) ∈ D ,对应的函数值为 z = f (x, y) 。这样,以 x 为横坐标、 y 为纵坐标、z = f (x, y) 为竖坐标在空间就确定一点 M (x, y,z) 。当(x, y)遍取 D 上的一切点时,得到一个空间点集 {(x, y,z) z = f (x, y),(x, y) ∈ D}, 这个点集称为二元函数 z = f (x, y) 的图形(图 8-5)。通常我们也说二元函数的图形是一张 曲面。 二元函数的图形通常是一张曲面. z = f (x, y) D x y z O • M x y P 例如,由空间解析几何知道,线形函数 z = ax + by + c 的图形是一张平面;由方程 2 2 2 2 x + y + z = a 所确定的函数 z = f (x, y) 的图形是球心在圆点、半径的为 a 球面,它的 定义域是圆形闭区域 {( , ) } 2 2 2 D = x y x + y ≤ a 。 在 D 的内部任一点(x, y)处,这函数有 两个对应值,一个为 2 2 2 a − x − y ,另一个为— 2 2 2 a − x − y 。因此,这是多值函数。 我们把它分成两个单值函数: 2 2 2 z = a − x − y 及 2 2 2 z = − a − x − y ,前者表示上半 球面,后者表示下半球面。以后除了对多元函数另做声明外,总假定所讨论的函数是单值的; 如果遇到多值函数,可以把它拆成几个单值函数后再分别加以讨论。 图 8-3 图 8-4