
高等数学C上课程基本情况1、课程编号:1131000564课程总学时:4课程学分:必修课程分类:秋开课学期:秀开课单位:理学学院数学适用专业:农学、园艺、园林、植保、动物医学、动物科学、化学、社会、农村发展、水产等所需先修课:无课程负责人:二、课程目标:1、课程总目标:高等数学C(上)课程是农学、动物科学及人文发展各专业的必修基础课。通过本课程的学习,学生将系统地获得微积分的基础理论和基本知识、掌握微积分的运算方法,为学生学习后继课程和解决实际问题提供必要的数学基础知识及常用的数学方法。课程的主要内容包括极限理论、一元函数微分学、一元函数积分学、微分方程。要求必须深刻理解一元微积分的基本概念,熟练掌握导数和积分的计算方法,并能了解它们在几何与物理上的简单应用,微分方程则不追求严格的论证和推导。注重基本运算的训练,不追求过分复杂的计算和变换。教学中要逐步培养学生具有比较熟练的基本运算能力、自学能力、抽象概括问题的能力,综合运用所学知识去分析和解决问题。2、课程分目标:课程分目标1:函数的连续性了解极坐标概念,掌握基本初等函数性质,掌握数列的极限和函数的极限的定义,了解函数极限的性质。掌握无穷小与无穷大概念,熟练掌握极限的运算定理和两个重要极限,了解函数的连续性课程分目标2:导数与微分深刻理解导数的概念及其意义,熟练掌握初等函数的导数公式,掌握函数的求导法则,会求隐函数、参数方程所确定的函数的导数,了解微分和高阶导数的概念。1
1 高等数学 C 上 一、 课程基本情况 课程编号:11310005 课程总学时: 64 课程学分: 4 课程分类: 必修 开课学期: 秋 开课单位: 理学 学院 数学 系 适用专业: 农学、园艺、园林、植保、动物医学、动物科学、化学、社会、农村发展、水产等 所需先修课:无 课程负责人: 二、课程目标: 1、课程总目标: 高等数学 C(上)课程是农学、动物科学及人文发展各专业的必修基础课。通过本课程的学习, 学生将系统地获得微积分的基础理论和基本知识、掌握微积分的运算方法,为学生学习后继课程和解 决实际问题提供必要的数学基础知识及常用的数学方法。课程的主要内容包括极限理论、一元函数微 分学、一元函数积分学、微分方程。要求必须深刻理解一元微积分的基本概念,熟练掌握导数和积分 的计算方法,并能了解它们在几何与物理上的简单应用,微分方程则不追求严格的论证和推导。注重 基本运算的训练,不追求过分复杂的计算和变换。 教学中要逐步培养学生具有比较熟练的基本运算能力、自学能力、抽象概括问题的能力,综合运 用所学知识去分析和解决问题。 2、课程分目标: 课程分目标 1: 函数的连续性 了解极坐标概念,掌握基本初等函数性质,掌握数列的极限和函数的极限的定义,了解函数极限的性 质。掌握无穷小与无穷大概念,熟练掌握极限的运算定理和两个重要极限,了解函数的连续性。 课程分目标 2: 导数与微分 深刻理解导数的概念及其意义,熟练掌握初等函数的导数公式,掌握函数的求导法则,会求隐函数、 参数方程所确定的函数的导数,了解微分和高阶导数的概念
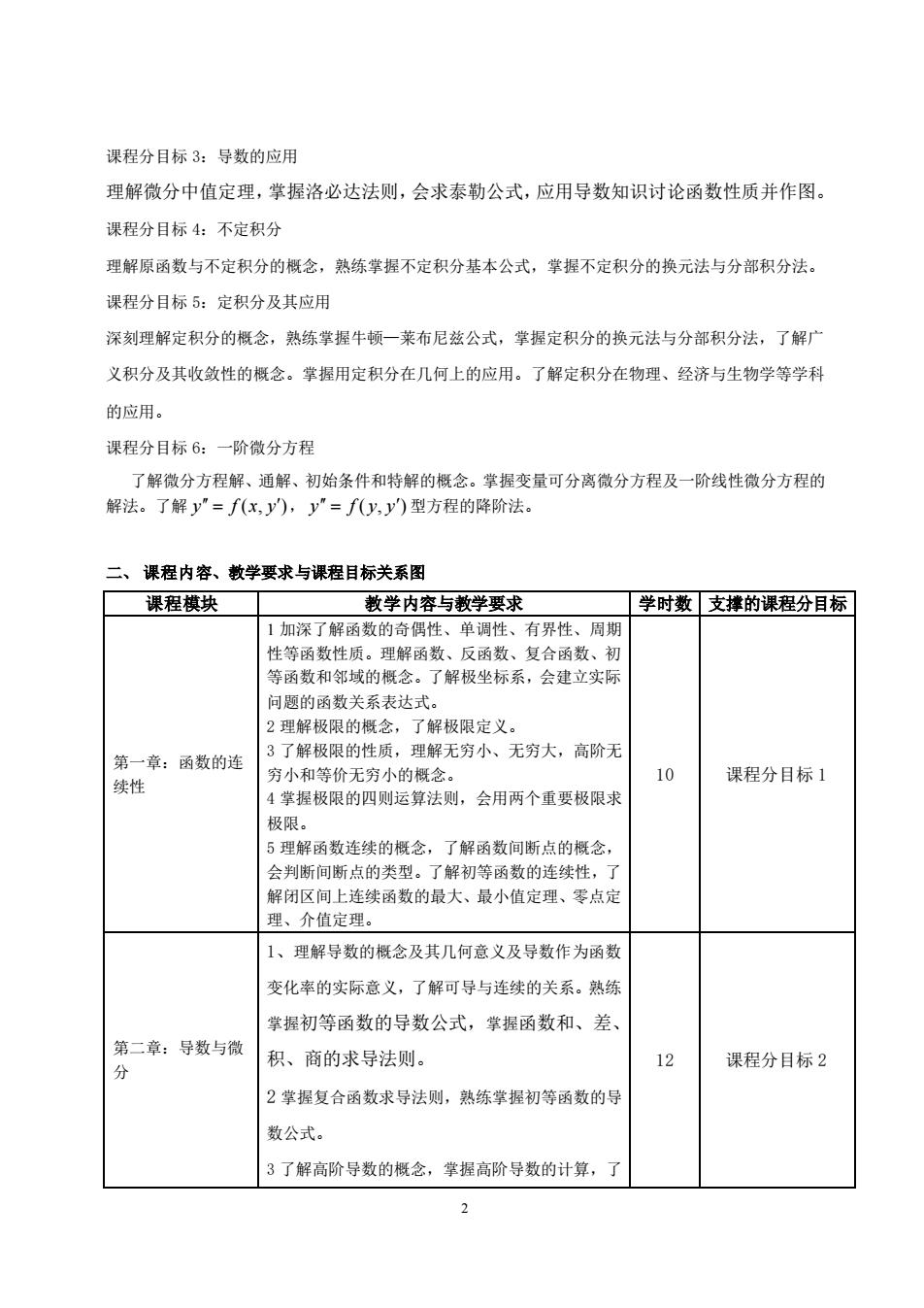
课程分目标3:导数的应用理解微分中值定理,掌握洛必达法则,会求泰勒公式,应用导数知识讨论函数性质并作图。课程分目标4:不定积分理解原函数与不定积分的概念,熟练掌握不定积分基本公式,掌握不定积分的换元法与分部积分法课程分目标5:定积分及其应用深刻理解定积分的概念,熟练掌握牛顿一莱布尼兹公式,掌握定积分的换元法与分部积分法,了解广义积分及其收敛性的概念。掌握用定积分在几何上的应用。了解定积分在物理、经济与生物学等学科的应用。课程分目标6:一阶微分方程了解微分方程解、通解、初始条件和特解的概念。掌握变量可分离微分方程及一阶线性微分方程的解法。了解y"=f(x,y),y"=f(y,y)型方程的降阶法。二、课程内容、教学要求与课程目标关系图课程模块教学内容与教学要求学时数支撑的课程分目标1加深了解函数的奇偶性、单调性、有界性、周期性等函数性质。理解函数、反函数、复合函数、初等函数和邻域的概念。了解极坐标系,会建立实际问题的函数关系表达式。2理解极限的概念,了解极限定义。3了解极限的性质,理解无穷小、无穷大,高阶无第一章:函数的连10课程分目标1穷小和等价无穷小的概念。续性4掌握极限的四则运算法则,会用两个重要极限求极限。5理解函数连续的概念,了解函数间断点的概念,会判断间断点的类型。了解初等函数的连续性,了解闭区间上连续函数的最大、最小值定理、零点定理、介值定理。1、理解导数的概念及其几何意义及导数作为函数变化率的实际意义,了解可导与连续的关系。熟练掌握初等函数的导数公式,掌握函数和、差、第二章:导数与微积、商的求导法则。12课程分目标2分2掌握复合函数求导法则,熟练掌握初等函数的导数公式。3了解高阶导数的概念,掌握高阶导数的计算,了2
2 课程分目标 3:导数的应用 理解微分中值定理,掌握洛必达法则,会求泰勒公式,应用导数知识讨论函数性质并作图。 课程分目标 4:不定积分 理解原函数与不定积分的概念,熟练掌握不定积分基本公式,掌握不定积分的换元法与分部积分法。 课程分目标 5:定积分及其应用 深刻理解定积分的概念,熟练掌握牛顿—莱布尼兹公式,掌握定积分的换元法与分部积分法,了解广 义积分及其收敛性的概念。掌握用定积分在几何上的应用。了解定积分在物理、经济与生物学等学科 的应用。 课程分目标 6:一阶微分方程 了解微分方程解、通解、初始条件和特解的概念。掌握变量可分离微分方程及一阶线性微分方程的 解法。了解 y = f (x, y), y = f ( y, y) 型方程的降阶法。 二、 课程内容、教学要求与课程目标关系图 课程模块 教学内容与教学要求 学时数 支撑的课程分目标 第一章:函数的连 续性 1 加深了解函数的奇偶性、单调性、有界性、周期 性等函数性质。理解函数、反函数、复合函数、初 等函数和邻域的概念。了解极坐标系,会建立实际 问题的函数关系表达式。 2 理解极限的概念,了解极限定义。 3 了解极限的性质,理解无穷小、无穷大,高阶无 穷小和等价无穷小的概念。 4 掌握极限的四则运算法则,会用两个重要极限求 极限。 5 理解函数连续的概念,了解函数间断点的概念, 会判断间断点的类型。了解初等函数的连续性,了 解闭区间上连续函数的最大、最小值定理、零点定 理、介值定理。 10 课程分目标 1 第二章:导数与微 分 1、理解导数的概念及其几何意义及导数作为函数 变化率的实际意义,了解可导与连续的关系。熟练 掌握初等函数的导数公式,掌握函数和、差、 积、商的求导法则。 2 掌握复合函数求导法则,熟练掌握初等函数的导 数公式。 3 了解高阶导数的概念,掌握高阶导数的计算,了 12 课程分目标 2
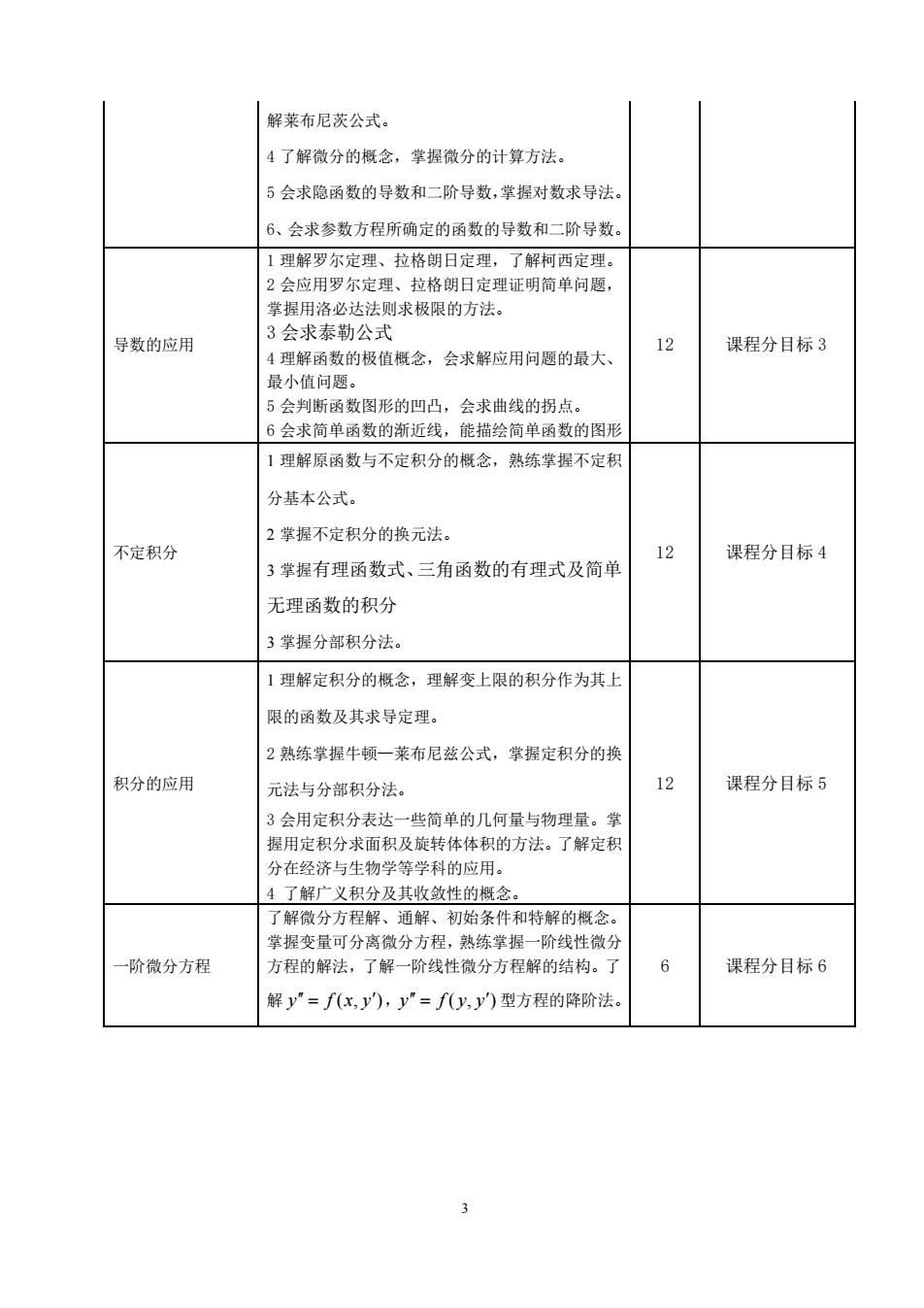
解莱布尼茨公式。4了解微分的概念,掌握微分的计算方法。5会求隐函数的导数和二阶导数,掌握对数求导法。6、会求参数方程所确定的函数的导数和二阶导数。1理解罗尔定理、拉格朗日定理,了解柯西定理。2会应用罗尔定理、拉格朗日定理证明简单问题,掌握用洛必达法则求极限的方法。3会求泰勒公式12课程分目标3导数的应用4理解函数的极值概念,会求解应用问题的最大、最小值问题。5会判断函数图形的凹凸,会求曲线的拐点。6会求简单函数的渐近线,能描绘简单函数的图形1理解原函数与不定积分的概念,熟练掌握不定积分基本公式。2掌握不定积分的换元法。12不定积分课程分目标43掌握有理函数式、三角函数的有理式及简单无理函数的积分3掌握分部积分法。1理解定积分的概念,理解变上限的积分作为其上限的函数及其求导定理。2熟练掌握牛顿一莱布尼兹公式,掌握定积分的换12课程分目标5积分的应用元法与分部积分法。3会用定积分表达一些简单的几何量与物理量。掌握用定积分求面积及旋转体体积的方法。了解定积分在经济与生物学等学科的应用。4了解广义积分及其收敛性的概念。了解微分方程解、通解、初始条件和特解的概念。掌握变量可分离微分方程,熟练掌握一阶线性微分6课程分目标6一阶微分方程方程的解法,了解一阶线性微分方程解的结构。了解y"=f(x,y),y"=f(y,y')型方程的降阶法。3
3 解莱布尼茨公式。 4 了解微分的概念,掌握微分的计算方法。 5 会求隐函数的导数和二阶导数,掌握对数求导法。 6、会求参数方程所确定的函数的导数和二阶导数。 导数的应用 1 理解罗尔定理、拉格朗日定理,了解柯西定理。 2 会应用罗尔定理、拉格朗日定理证明简单问题, 掌握用洛必达法则求极限的方法。 3 会求泰勒公式 4 理解函数的极值概念,会求解应用问题的最大、 最小值问题。 5 会判断函数图形的凹凸,会求曲线的拐点。 6 会求简单函数的渐近线,能描绘简单函数的图形 12 课程分目标 3 不定积分 1 理解原函数与不定积分的概念,熟练掌握不定积 分基本公式。 2 掌握不定积分的换元法。 3 掌握有理函数式、三角函数的有理式及简单 无理函数的积分 3 掌握分部积分法。 12 课程分目标 4 积分的应用 1 理解定积分的概念,理解变上限的积分作为其上 限的函数及其求导定理。 2 熟练掌握牛顿—莱布尼兹公式,掌握定积分的换 元法与分部积分法。 3 会用定积分表达一些简单的几何量与物理量。掌 握用定积分求面积及旋转体体积的方法。了解定积 分在经济与生物学等学科的应用。 4 了解广义积分及其收敛性的概念。 12 课程分目标 5 一阶微分方程 了解微分方程解、通解、初始条件和特解的概念。 掌握变量可分离微分方程,熟练掌握一阶线性微分 方程的解法,了解一阶线性微分方程解的结构。了 解 y = f (x, y),y = f ( y, y) 型方程的降阶法。 6 课程分目标 6
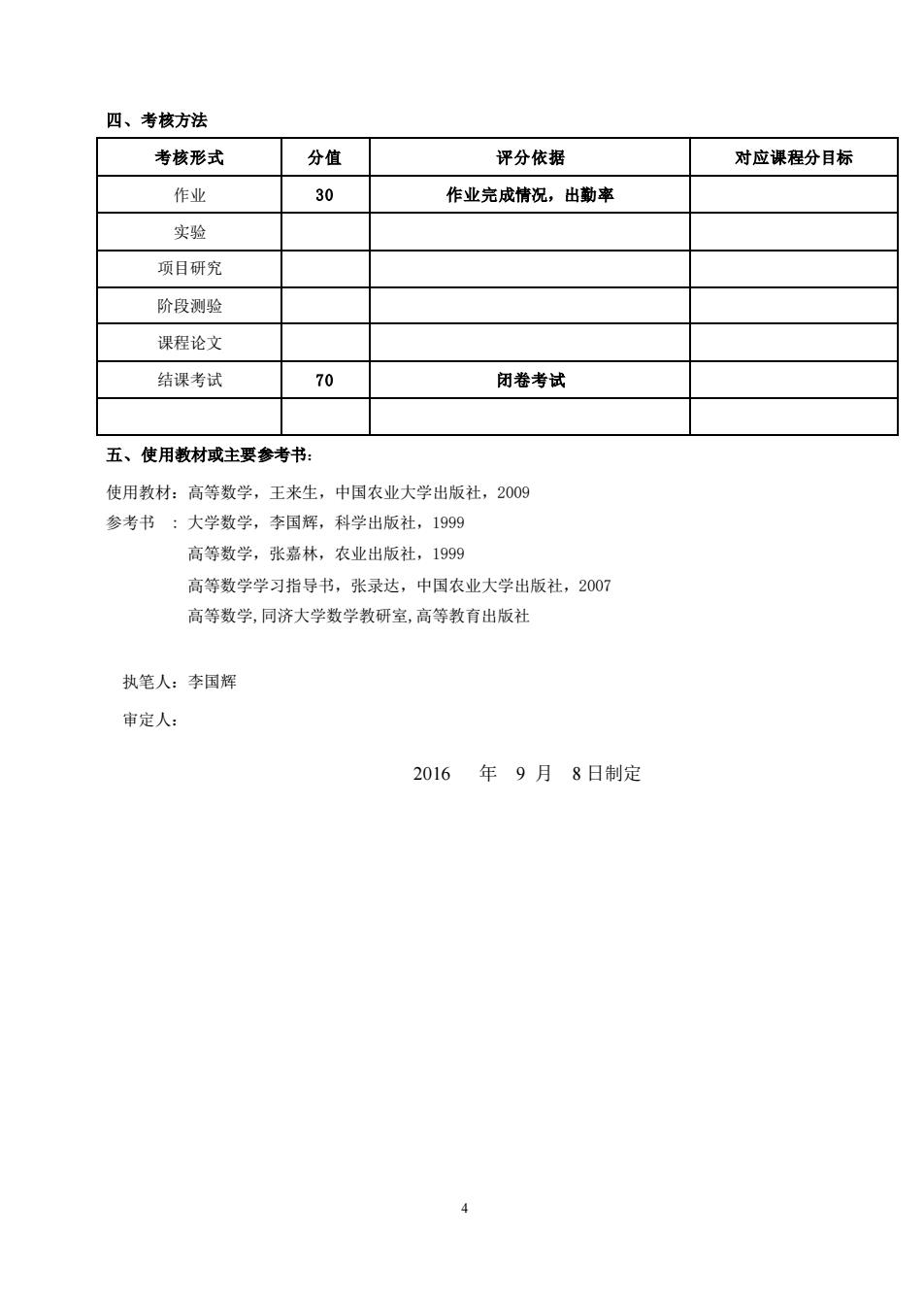
四、考核方法分值考核形式评分依据对应课程分目标作业30作业完成情况,出勤率实验项目研究阶段测验课程论文70结课考试闭卷考试五、使用教材或主要参考书:使用教材:高等数学,王来生,中国农业大学出版社,2009参考书:大学数学,李国辉,科学出版社,1999高等数学,张嘉林,农业出版社,1999高等数学学习指导书,张录达,中国农业大学出版社,2007高等数学,同济大学数学教研室,高等教育出版社执笔人:李国辉审定人:2016年9月8日制定4
4 四、考核方法 考核形式 分值 评分依据 对应课程分目标 作业 30 作业完成情况,出勤率 实验 项目研究 阶段测验 课程论文 结课考试 70 闭卷考试 五、使用教材或主要参考书: 使用教材:高等数学,王来生,中国农业大学出版社,2009 参考书 : 大学数学,李国辉,科学出版社,1999 高等数学,张嘉林,农业出版社,1999 高等数学学习指导书,张录达,中国农业大学出版社,2007 高等数学,同济大学数学教研室,高等教育出版社 执笔人:李国辉 审定人: 2016 年 9 月 8 日制定

(Attachment:formatoftheteachingsyllabus)English name of the course1. Basic informationCourse code:64Total teaching hours:,amongwhichhours for lectures,hoursforexperiments,hours foron-line teaching.Credits: 4Typeofthecourse:(compulsoryorelective):compulsoryTeachingterms: (spring,summerorautumn) : autumnOwner of the course: (Teaching group, department, college) : Department of applied mathematics.collegeofmathematicsMajors applicable:Agriculture, horticulture,garden architecture,plant protection,Veterinary Medicine,Animal Science, Chemistry,Society,Rural Area Development,AquaculturePrerequisites:NonePerson in charge ofthe course:2.Course Objectives(1)GeneralAimAdvanced Mathematics C(I) is a compulsorybase course for themajors of agriculture,animal science and human development. Through the study of this course, students will learnsystematically basic theory and fundamental knowledge of calculus, master the calculationmethods in calculus, and prepare necessary mathematical basic knowledge and commonmathematical methods for the subsequent courses and solving practical problems. The maincontent of the course include:limit theory, differentiation of functions of one variable,integration of functions of one variable, and differential equations. Require mandatorilyto understand deeply the basic concepts in calculus of functions of onevariable,to masterproficiently the calculation methods of derivative and integrals, and toknowtheir simpleapplications in geometry and physics, but not to argue or derive rigorously. Emphasize ontraining of basic calculations,but not on too complicated computation or transformations.In teaching, foster the students gradually the basic calculation ability, self-studyability,abstraction and summarization ability,and to apply comprehensively theknowledgelearned to analyze and solve problems.(2)BranchObjectivesTheFirst one:Continuityof functions5
5 (Attachment: format of the teaching syllabus) English name of the course 1. Basic information Course code: Total teaching hours: _64_, among which_ hours for lectures, _ hours for experiments, _hours for on-line teaching. Credits: 4 Type of the course: (compulsory or elective): compulsory Teaching terms: (spring, summer or autumn) : autumn Owner of the course: (Teaching group, department, college) : Department of applied mathematics, college of mathematics Majors applicable: Agriculture, horticulture, garden architecture, plant protection, Veterinary Medicine, Animal Science, Chemistry, Society, Rural Area Development, Aquaculture Prerequisites: None Person in charge of the course: 2. Course Objectives (1)General Aim Advanced Mathematics C(I) is a compulsory base course for the majors of agriculture, animal science and human development. Through the study of this course, students will learn systematically basic theory and fundamental knowledge of calculus, master the calculation methods in calculus, and prepare necessary mathematical basic knowledge and common mathematical methods for the subsequent courses and solving practical problems. The main content of the course include: limit theory, differentiation of functions of one variable, integration of functions of one variable, and differential equations. Require mandatorily to understand deeply the basic concepts in calculus of functions of one variable, to master proficiently the calculation methods of derivative and integrals, and to know their simple applications in geometry and physics, but not to argue or derive rigorously. Emphasize on training of basic calculations, but not on too complicated computation or transformations. In teaching, foster the students gradually the basic calculation ability, self-study ability, abstraction and summarization ability, and to apply comprehensively the knowledge learned to analyze and solve problems. (2)Branch Objectives The First one:Continuity of functions