
第五章定积分$5.1定积分的概念教学目的:理解定积分的定义教学重点:连续变量的累积教学难点:连续变量的累积教学内容:一、定积分举例:1、曲边梯形面积设y=f(x)在[a,b]上非负,连续,由直线x=a,x=b,y=0及曲线y=f(x)所围成的图形,称为曲边梯形。求面积:在区间[a,b]中任意插入若干个分点a=xo<x<x2<xn-1<x,=b,把[a,b]分成n个小区间[o,x],[x,X2], .-[xn-1,x,],它们的长度依次为:Ax,=Xi-Xo,Ax, =X2-xi,",Ax,=X,-Xn-1经过每一个分点作平行于y轴的直线段,把曲边梯形分成n个窄曲边梯形在每个小区间[xi-1,x,]上任取一点5,以[xi-,x,]为底,F(5)为高的窄边矩形近似替代第i个窄边梯形(i=1,2,n),把这样得到的n个窄矩形面积之和作为所求曲边梯形面积A的近似值,即A= f(5,)Ax, + f(5)Ar, +..+ f(5,)Ax-2 f(5,)Ax,设=max(Ax,Ax2…Ax→0时,可得曲边梯形的面积A = lim f(5)Ax,A-01=1140
140 第五章 定积分 §5.1 定积分的概念 教学目的:理解定积分的定义 教学重点:连续变量的累积 教学难点:连续变量的累积 教学内容: 一、定积分举例: 1、 曲边梯形面积 设 y = f (x)在 [ ] a,b 上非负,连续,由直线 x = a, x = b, y = 0 及曲线 y = f (x) 所围成的图形,称为曲边梯形。 求面积: 在区间 [a,b] 中任意插入若干个分点 a = x0 < x1 < x2 " < xn−1 < xn = b ,把[a,b]分成 n 个小区间 [ 0 1 x , x ],[ 1 2 x , x ], . [ n n x , x −1 ], 它们的长度依次为: 1 1 0 2 2 1 1 , , , Δ = − Δ = − Δ n = n − n− x x x x x x " x x x 经过每一个分点作平行于 y 轴的直线段,把曲边梯形分成 n 个窄曲边梯形, 在每个小区间[ i i x , x −1 ]上任取一点ξ i ,以[ i i x , x −1 ]为底, ( )i f ξ 为高的窄边矩形近 似替代第i 个窄边梯形(i=1,2,.,n),把这样得到的 n 个窄矩形面积之和作为所求 曲边梯形面积 A 的近似值,即 i n n A ≈ f ( )Δx + f ( )Δx + + f ( )Δx ξ 1 ξ 2 2 " ξ =∑= Δ n i i i f x 1 (ξ ) 设λ = max{Δx1 ,Δx2 ,"Δxn },λ → 0时,可得曲边梯形的面积 ∑= → = Δ n i i i A A f x 1 0 lim (ξ )

2、变速直线运动的路程设某物体作直线运动,已知速度v=v(t)是时间间隔[T,T,]上t的连续函数,且vt≥O),计算在这段时间内物体所经过的路积S在[T,T,]内任意插入若干个分点T =to <t, <t, <...tn-- <t, =T,把[T,T,]分成n个小段[to,t], [h,t], ,[tu-,t,]各小段时间长依次为:At, =t,-to,At2=t2-t,",At,=t,-tn-l,相应各段的路程为:AS1,AS2,",AS在[ti-1,t,]上任取一个时刻T,(ti-I≤T,≤t),以T,时的速度v(T)来代替[ti-I,t,]上各个时刻的速度,则得:AS, ~ V(T)At)(i=1,2,,n)进一步得到:S~v(T,)At +v(T,)At, +...+v(T,)AT,=Zv(T,)A1)i=l设元=maxAt,At.,A当a→0时得:S = limZv(T,)At201二、定积分的定义由上述两例可见,虽然所计算的量不同,但它们都决定于一人函数及其自变量的变化区间,其次它们的计算方法与步骤都相同,即归纳为一种和式极限,即面积A=limf(5)Ax,,1→>0i=l141
141 2、 变速直线运动的路程 设某物体作直线运动,已知速度v = v(t) 是时间间隔[ 1 2 T ,T ]上 t 的连续函数, 且v(t ≥ 0) ,计算在这段时间内物体所经过的路积 S 在[ 1 2 T ,T ]内任意插入若干个分点 1 0 1 2 1 T2 T t t t t t = < < < " n− < n = 把[ 1 2 T ,T ]分成 n 个小段 [ 0 1 t ,t ],[ 1 2 t ,t ],., [ n n t ,t −1 ] 各小段时间长依次为: , , , , Δ 1 = 1 − 0 Δ 2 = 2 − 1 Δ n = n − n−1 t t t t t t " t t t 相应各段的路程为: ΔS ΔS ΔSn , , , 1 2 " 在[ i i t ,t −1 ]上任取一个时刻 ( ) i i 1 i i T t ≤ T ≤ t − ,以Ti 时的速度 ( ) Ti v 来代替[ i i t ,t −1 ] 上各个时刻的速度,则得: i i i Δ S ≈ v (T ) Δ t ) (i = 1,2,",n 进一步得到: n n S ≈ v(T )Δt + v(T )Δt + + v(T )Δt 1 1 2 2 " =∑= Δ n i v T t 1 1 1 ( ) 设λ = max{ } Δt1 ,Δt2 ,",Δtn ,当λ → 0 时, 得: ∑= → = Δ n i i S v T t 1 0 lim ( ) λ 二、定积分的定义 由上述两例可见,虽然所计算的量不同,但它们都决定于一人函数及其自变 量的变化区间,其次它们的计算方法与步骤都相同,即归纳为一种和式极限,即 面积 ∑= → = Δ n i i i A f x 1 0 lim (ξ ) λ

路程S=limZv(T,)At,1→0将这种方法加以精确叙述得到定积化的定义定义设函数f(x)在[a,b]上有界,在[a,b]中任意插入若干个分点a=X<x <x2 <...<xn- <x,=b把区间[a,b]分成n个小区间[xo,x],[x,x2],,[xn-1,x,],各个小区间的长度依次为Ax=x-xo,Ax2=x2-x,,Ax,=x,-Xn-1在每个小区间[x-1,x,]上任取一点s(x-≤6,≤x,),作函数值f(c)与小区间长度Ax,的乘积f(s,)Ax,(i=1,2,.,n),并作出和S=2f(6,)Ax,记=max(Axi,Ar2,,Ar},如果不论对[a,b]怎样分法,也不论在小区间[xi-1,x,]上点s怎样取法,只要当入→1时,和S总趋于确定的极限1,这时我们称这个极限1为函数f(x)在区间[a,b)上的定积分(简称积分),记作["f(x)dx,即I(x)dx=I=lim之(s,)Ax,20其中f(x)叫做被积函数,f(x)dx叫做被积表达式,x叫做积分变量,a叫做积分下限,b叫做积分上限,[a,b]叫做积分区间注意:积分与积分变量无关,即:"(x)dx=I"()dt =I'(u)du函数可积的两个充分条件:定理1设f(x)在[a,b]上连续,则f(x)在[a,b]上可积。定理2设f(x)在[a,b]上有累,且只有有限个间断点,则f(x)在[a,b]上可积。例:利用定积分定义计算【x2dx142
142 路程 ∑= → = Δ n i i i S v T t 1 0 lim ( ) λ . 将这种方法加以精确叙述得到定积化的定义 定义 设函数 f (x)在[a,b]上有界,在[a,b]中任意插入若干个分点 a = x0 < x1 < x2 < " < xn−1 < xn = b 把区间[a,b]分成n 个小区间 ], [ , ],[ , ], ,[ , 0 1 1 2 n 1 n x x x x x x " − 各个小区间的长度依次为 1 1 0 2 2 1 1 , , , Δ = − Δ = − Δ n = n − n− x x x x x x " x x x . 在每个小区间[ i i x , x −1 ]上任取一点 i i i i x ≤ ≤ x − ε ε 1 ( ),作函数值 ( )i f ε 与小区间长度 i Δx 的乘积 f ( ) x (i 1,2, ,n), ε i Δ i = " 并作出和 ∑= = Δ n i i i S f x 1 (ε ) . 记 max{ , , , } 1 2 n λ = Δx Δx " Δx ,如果不论对[a,b]怎样分法,也不论在小区间[ i i x , x −1 ] 上点 i ε 怎样取法,只要当λ →1时,和 S 总趋于确定的极限 I ,这时我们称这个极限 I 为函数 f (x) 在区间[a,b]上的定积分(简称积分),记作 ∫ b a f (x)dx ,即 ∫ b a f (x)dx = I = ∑= → Δ n i i i f x 1 0 lim (ε ) λ , 其中 f (x) 叫做被积函数, f (x)dx 叫做被积表达式, x 叫做积分变量, a 叫做积分下 限,b 叫做积分上限, [a,b]叫做积分区间. 注意:积分与积分变量无关,即: ∫ ∫∫ = = b a b a b a f (x)dx f (t)dt f (u)du 函数可积的两个充分条件: 定理 1 设 f (x)在[a,b]上连续,则 f (x) 在[a,b]上可积。 定理 2 设 f (x)在[a,b]上有累,且只有有限个间断点,则 f (x)在[a,b]上可积。 例:利用定积分定义计算 ∫ 1 0 2 x dx
解:f(x)=x在[0,1]上连续函数,故可积,因此为方便计算,我们可以1对[0,1]n等分,分点x,=,i=1,2n-15取相应小区间的右端点,故n2 f(5)Ar, =2A,-2x,Ax,台i=li=lZ(一)Ti-3/nn=lnis11n(n + 1)(2n + 1)n36(+)(2+)6nn入一0时(即n一80时),由定积分的定义得:x'dx=!3例:用定义计算由抛物线y=x2直线x=1和x轴所围成的曲边梯形面积I解:将[0,1]分成n等分,分点为x,=,i=1,2...nVn,i=1,2..n小区间[x-,x,]的长度Ax,=V:n取5,=x,i=1,2..-n,2F(5)Ax, =254 =2xAx =13nn=(n)1i=l-112() -111/2+11+-=1660210=→T rdx=lm≥54x,=lim(1+=2+=-1-→04n→6nni=l对于任一确定的自然数n.积分和r'dx ~Zf(5)Ax =-2+1+当n取不同值时,x2dx近似值精度不同.n取得越大,近似程度越好,143
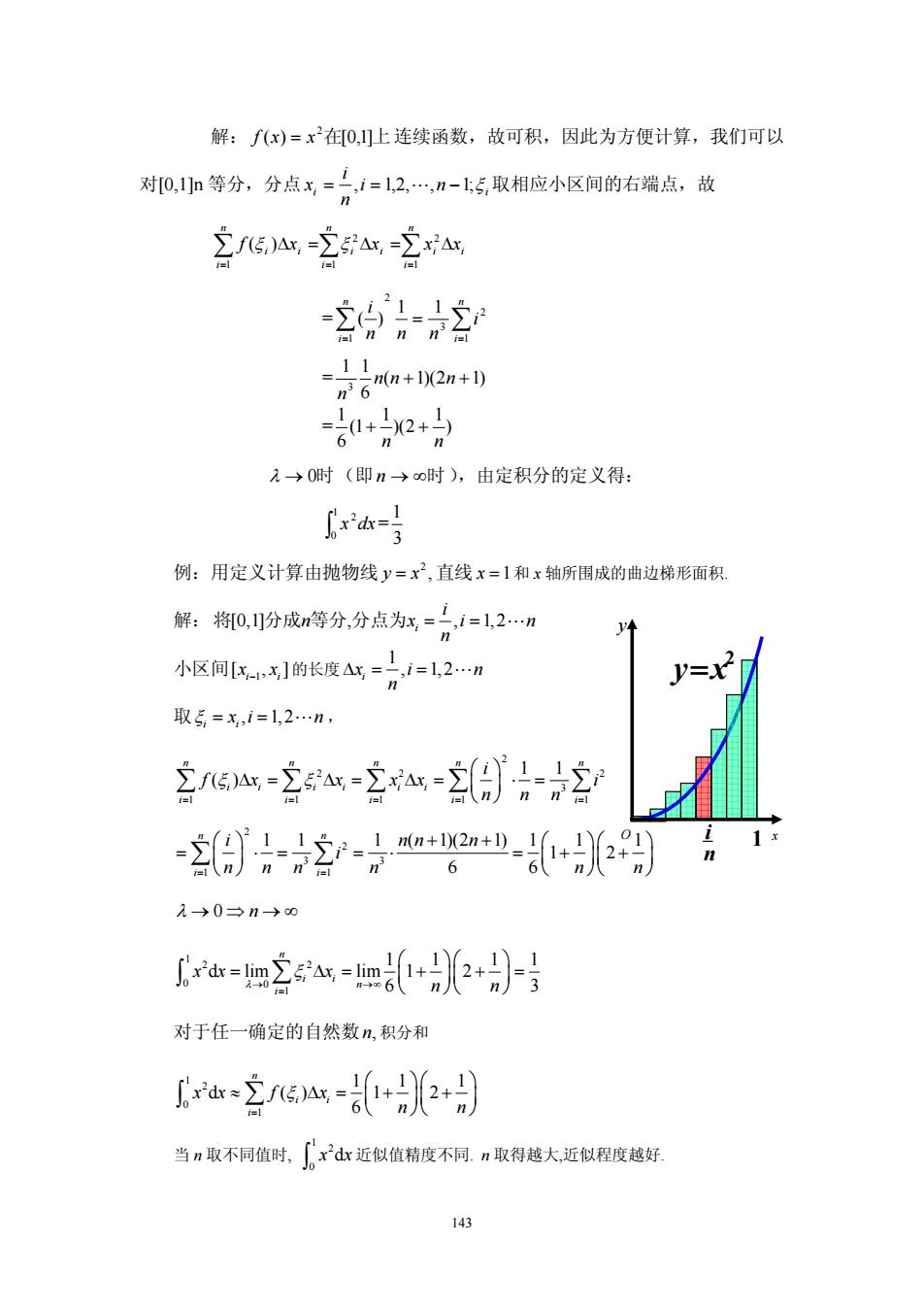
143 解: 上 ( ) 在[0,1] 2 f x = x 连续函数,故可积,因此为方便计算,我们可以 对[0,1]n 等分,分点 i n i i n i x = , = 1,2,", −1;ξ 取相应小区间的右端点,故 ∑ ∑ ∑ = = = Δ = Δ = Δ n i i i n i i i n i i i f x x x x 1 2 1 2 1 (ξ ) ξ =∑ ∑ = = = n i n i i n n n i 1 2 3 2 1 1 1 ( ) = ( 1)(2 1) 6 1 1 3 n n + n + n = ) 1 )(2 1 (1 6 1 n n + + λ → 0时(即n → ∞时),由定积分的定义得: ∫ 1 0 2 x dx = 3 1 例:用定义计算由抛物线 2 y = x , 直线 x =1和 x 轴所围成的曲边梯形面积. 解: [0,1] , , 1,2 i i n xi n n 将 分成 等分 分点为 = = " 小区间 1 [ ,] i i x x − 的长度 1 , 1,2 i x i n n Δ= = " 取 , 1,2 i i ξ = = x i n " , 2 2 1 11 ( ) n nn i i i i ii i ii f ξ ξ x x xx = == ∑ ∑∑ Δ= Δ= Δ 2 2 3 1 1 1 1 n n i i i i = = n nn ⎛ ⎞ = ⋅= ⎜ ⎟ ⎝ ⎠ ∑ ∑ 2 2 3 3 1 1 1 1 1 ( 1)(2 1) 1 1 1 1 2 6 6 n n i i i nn n i = = n nn n n n ⎛ ⎞ ⎛ ⎞⎛ ⎞ + + = ⋅= = ⋅ = + + ⎜ ⎟ ⎜ ⎟⎜ ⎟ ⎝ ⎠ ⎝ ⎠⎝ ⎠ ∑ ∑ λ → ⇒ →∞ 0 n 1 2 2 0 0 1 1 1 11 d lim lim 1 2 6 3 n i i n i xx x λ n n ξ → →∞ = ⎛ ⎞⎛ ⎞ = Δ= + + = ⎜ ⎟⎜ ⎟ ⎝ ⎠⎝ ⎠ ∫ ∑ 对于任一确定的自然数n, 积分和 1 2 0 1 11 1 d () 1 2 6 n i i i xx f x n n ξ = ⎛ ⎞⎛ ⎞ ≈ Δ= + + ⎜ ⎟⎜ ⎟ ⎝ ⎠⎝ ⎠ ∫ ∑ 当 n 取不同值时, 1 2 0 x dx ∫ 近似值精度不同. n 取得越大,近似程度越好. n i 2 y=x 1 y O x
例:用定积分的几何意义计算2xdx,并求由x=-6,x=2,y=0及y=2x所围成图形的面积(如图)解:作y=2x在-6≤x≤2上的y图形,由定积分几何意义可知B2xdx就等于△OAB的面积减去△OCD的面积(在x轴下0A6一方的面积为负)C2AOAB的面积=×2×4=42△OCD的面积=-x6x12=3622xdx=4-36=-32D再求由直线x=-6,x=2,y=0及y=2x所围成图形的面积为:A=[",12x| dx =J~-2xdx+f,2xdx = -×6×12+=×2×4=4022小结①重述定积分的定义;②注意其中的两个“任意”③涉及对连续变量的累积,一般采用分割,近似求和,取极限的方法进而归结到求定积分。作业144
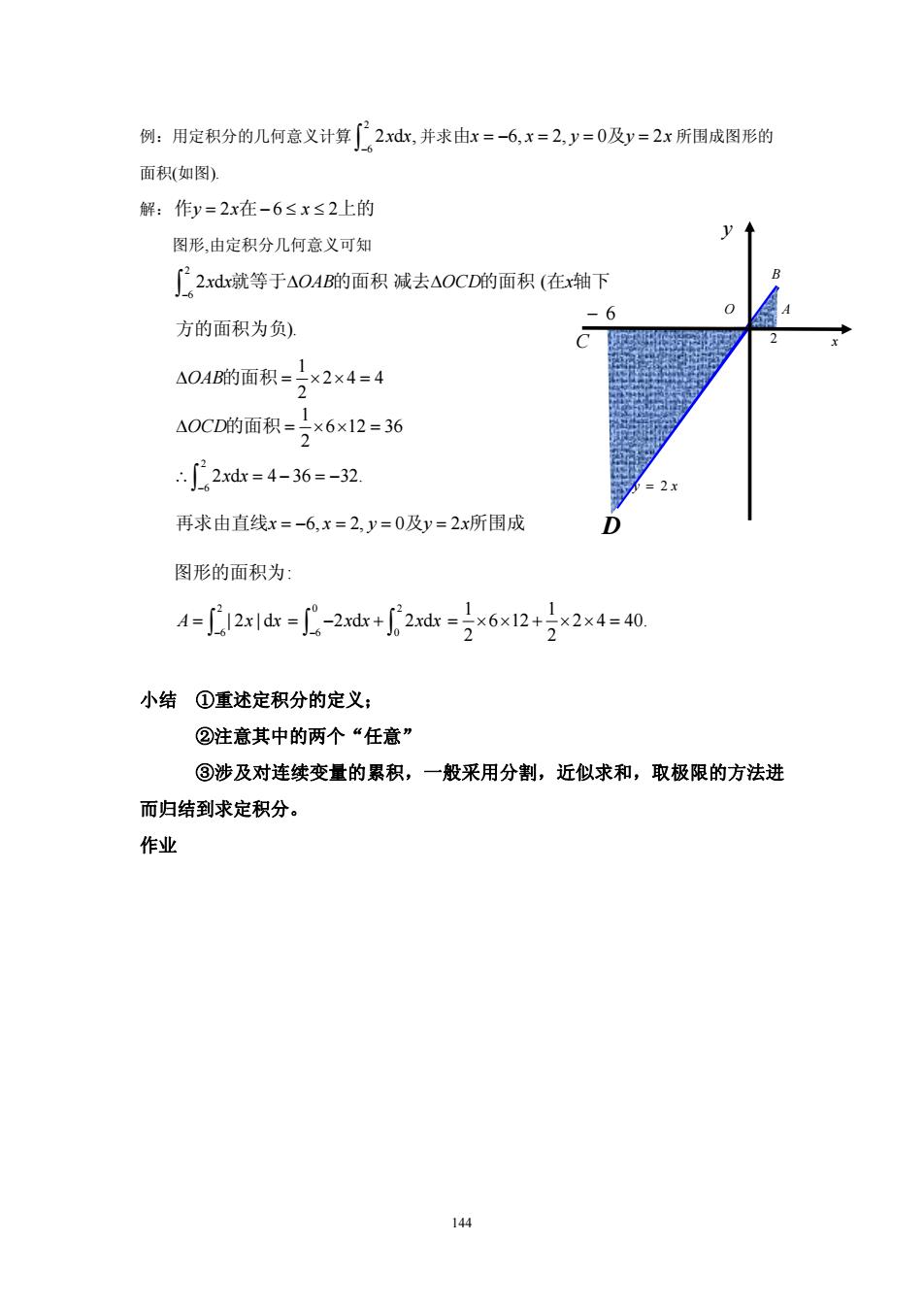
144 例:用定积分的几何意义计算 2 6 2d, x x ∫− 并求由 及 x = −= = = 6, 2, 0 2 x y yx 所围成图形的 面积(如图). 解:作 在 上的 yx x = −≤≤ 26 2 图形,由定积分几何意义可知 2 6 2 dx x OAB − Δ ∫ 就等于 的面积 减去 的面积 在 轴下 ΔOCD x ( 方的面积为负). 1 24 4 2 Δ = ×× = OAB的面积 1 6 12 36 2 Δ = ×× = OCD的面积 2 6 2 d 4 36 32. x x − ∴ = − =− ∫ 再求由直线 及 所围成 x x y yx = −= = = 6, 2, 0 2 图形的面积为: 2 6 A xx |2 |d − = ∫ 0 2 6 0 2d 2d x x xx − =− + ∫ ∫ 1 1 6 12 2 4 40. 2 2 = ×× + ×× = 小结 ①重述定积分的定义; ②注意其中的两个“任意” ③涉及对连续变量的累积,一般采用分割,近似求和,取极限的方法进 而归结到求定积分。 作业 y = 2 x A 2 − 6 x y O D B C