
3、若在D上,J(x,J)=1,为区域D的面积,则α= J[ 1dα = [[ doDD几何意义:高为1的平顶柱体的体积在数值上等于柱体的底面积。4、若在D上,F(x,J)≤Q(x,J),则有不等式J f(x, y)dg≤ JJ p(x, y)do特别地,由于-(x,≤(,)≤(,)],有J (x,y)d≤J[ If(x,y)] do5、【估值不等式】设M与m分别是F(x,J)在闭区域D上最大值和最小值,是M的面积,则m-o≤[l f(x,y)do<M.o6、【二重积分的中值定理】设函数(x,J)在闭区域D上连续,C是D的面积,则在D上至少存在一点(,n),使得Jf(x,y)dg=f(5, n).I =[(x2 +4y2 +9)do的值,D是圆域×2+≤4。例1、估计二重积分解:求被积函数f(x,J)=x2+4y2+9在区域D上可能的最值af=2x=0axaf=8y=0ay(0,0)是驻点,且(0,0)=9
3、若在 D 上, f (, ) x y ≡1,σ 为区域 D 的面积,则 σ = = ∫∫ ∫∫ 1d d σ σ D D 几何意义: 高为1的平顶柱体的体积在数值上等于柱体的底面积。 4、若在 D上, f (, ) (, ) x y ≤ϕ x y ,则有不等式 ∫∫ ∫∫ ≤ D D f (x, y)dσ ϕ(x, y)dσ 特别地,由于− f (x, y) ≤ f (x, y) ≤ f (x, y) ,有 f x y dσ f x y dσ D D ∫∫ ∫∫ ( , ) ≤ ( , ) 5、【估值不等式】 设 M 与m分别是 f (, ) x y 在闭区域 D上最大值和最小值,σ 是 M 的面积, 则 ∫∫ ⋅ ≤ ≤ ⋅ D m σ f (x, y)dσ M σ 6、【二重积分的中值定理】 设函数 f (, ) x y 在闭区域 D 上连续,σ 是 D 的面积,则在 D 上至少存在一 点(,) ξ η ,使得 ∫∫ = ⋅ D f (x, y) dσ f ( ξ,η ) σ 例 1、估计二重积分 = ∫∫ + + D I (x 4y 9)dσ 2 2 的值, D是圆域 x y 2 2 + ≤ 4 。 解: 求被积函数 9 ( , ) 4 2 2 f x y = x + y + 在区域 D上可能的最值 ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ = = = = 8 0 2 0 y y f x x f ∂ ∂ ∂ ∂ (,) 0 0 是驻点,且 f (,) 00 9 = ;

在边界上,(x,J)= x2 + 4(4 - x3)+ 9 = 25 - 3x(-2 ≤x≤2)13≤f(x,y)≤25Jmax =25, min = 9,于是有36元=9.4元≤1≤25.4元=100元例2、设D为圆域x+R,求二重积分R-x-dD解:z=/R2-x?-y2是上半球面,由二重积分的几何意义可知,上述积分等于上半球体的体积:2元RJJ R-x-'do=-3例3、比较积分I,=[[in(x+y)da,,=[[(x+y)"do,I,=[[(x+y)do的大小,DD其中D是由直线x=0.y=0.x+y=和x+y=1所围成的。2解:因为积分域D在直线x+y=1的下方,所以对任意点(x,J)eD,均有1≤x+y≤1,从而有x+y≥(x+y)2>0,而ln(x+y)<0,故由二重积分的2性质得,≤1≤13。例4、判断(In(x2+y)dxdy的正负号。rsx+by/s1解:当rx|+lyk1时,0<x +y ≤(Ix/+/yD2 ≤1故In(x +y°)≤0又当In(x? +y)<0Ix|+lyk1于是( In(x? + y°)dxdy<0rs1311s1例5、不作计算,估计I={[er+)da的值,其中D是椭圆闭区域:x?≤1,(0<b<a)Ob2
在边界上, ( , ) 4(4 ) 9 25 3 ( 2 2) 2 2 2 f x y = x + − x + = − x − ≤ x ≤ 13 ≤ f (x, y) ≤ 25 25 max f = , 9 min f = , 于是有 36π =9⋅ 4π ≤I ≤25⋅ 4π =100π 例 2、设 D 为圆域 22 2 x + ≤ y R ,求二重积分 222 d D Rxy − − σ ∫∫ 。 解: 222 z Rxy = −− 是上半球面, 由二重积分的几何意义可知,上述积分等于上半球体的体积: 222 3 2 d 3 D R −− = xy R σ π ∫∫ 例 3、比较积分 ∫∫ = + D I1 ln(x y)dσ , ∫∫ ∫∫ = + = + D D I (x y) dσ, I 3 (x y)dσ 2 2 的大小, 其中 D 是由直线 2 1 x = 0, y = 0, x + y = 和 x + y = 1所围成的。 解:因为积分域 D 在直线 x + y = 1的下方,所以对任意点(x, y) ∈ D ,均有 1 2 1 ≤ x + y ≤ ,从而有 ( ) 0 2 x + y ≥ x + y > ,而ln(x + y) < 0,故由二重积分的 性质得 1 2 3 I ≤ I ≤ I 。 例 4、判断 2 2 ||||1 ln( )d d rx y x y xy ≤+≤ + ∫∫ 的正负号。 解:当rx y ≤+< | | | |1时, 22 2 0 (| | | |) 1 <+≤ + ≤ xy x y 故 2 2 ln( ) 0 x y + ≤ 又当 | | | |1 x y + < 2 2 ln( ) 0 x y + < 于是 2 2 ||||1 ln( )d d 0 rx y x y xy ≤+≤ + < ∫∫ 例 5 、不作计算,估计 2 2 ( )d x y D I e σ + = ∫∫ 的值,其中 D 是椭圆闭区域: 2 2 2 2 1,(0 ) x y b a a b + ≤ <<

解:区域D的面积α=αb元在D上,0≤x2+?≤a?..1=e°<er+y'<e?g≤ [[e(r+y)dg≤g-eDab元 ≤ [[e(r+)dg ≤abre'D1.r例6、求lim-f(x,y)do-0元ptsp解:利用积分中值定理,即得:J f(x, )dg= f(5,n) J do= p"f(5,n)x?+y"sp?Y+y'sp?其中点(,n)是圆域x2+y≤p2内的一点。显然,当p→0时,点(5n)→(0,0)由函数的连续性知1rlim-f(x,y)da=lim f(,n)= f(0,0)p-0元p20-x*+y≤p?小结二重积分的定义(四步:分割、取近似、求和、取极限)二重积分的几何意义(曲顶柱体的体积)二重积分的性质(注意对称性质的用法)作业教材
解:区域 D 的面积σ = abπ 在 D 上, 222 ∵0 ≤ x + ≤ y a 22 2 0 1 x y a ee e + ∴ =≤ ≤ 22 2 ( )d x y a D σ σσ e e + ≤ ≤⋅ ∫∫ 22 2 ( )d x y a D ab e ab e π σ π + ≤ ≤ ∫∫ 例 6、求 222 2 0 1 lim ( , )d x y f xy ρ ρ σ → πρ + ≤ ∫∫ 解:利用积分中值定理,即得: 222 222 2 ( , )d ( , ) d ( , ) xy xy f xy f f ρ ρ σ ξ η σ πρ ξ η +≤ +≤ =⋅ = ∫∫ ∫∫ 其中点(,) ξ η 是圆域 22 2 x y + ≤ ρ 内的一点。 显然,当 ρ → 0时,点( , ) 0,0 ξ η → ( ) 由函数的连续性知 ( ) 222 2 0 0 1 lim ( , )d lim ( , ) 0,0 x y f xy f f ρ ρ ρ σ ξη → → πρ + ≤ = = ∫∫ 小结 二重积分的定义(四步:分割、取近似、求和、取极限) 二重积分的几何意义(曲顶柱体的体积) 二重积分的性质(注意对称性质的用法) 作业 教材

89.2二重积分的计算法教学目的:熟练掌握二重积分的计算方法教学重点:利用直角坐标和极坐标计算二重积分教学难点:化二重积分为二次积分的定限问题教学内容:利用二重积分的定义来计算二重积分显然是不实际的,二重积分的计算是通过两个定积分的计算(即二次积分)来实现的。一、利用直角坐标计算二重积分JJ f(x,y)do我们用几何观点来讨论二重积分D的计算问题。讨论中,我们假定 (x,J)≥0假定积分区域D可用不等式α≤x≤b(x)≤≤(x)表示,其中(x),2(x)在[a,b]上连续。JyIy=Φ2(αx)y=Φ,(x)y=(x)y=Φ(x)obbxoaxaJJ f(x, y)do的值等于以D为底,以曲面据二重积分的几何意义可知,Dz= f(x,y)为顶的曲项柱体的体积
§9.2 二重积分的计算法 教学目的:熟练掌握二重积分的计算方法 教学重点:利用直角坐标和极坐标计算二重积分 教学难点:化二重积分为二次积分的定限问题 教学内容: 利用二重积分的定义来计算二重积分显然是不实际的,二重积分的计算是通 过两个定积分的计算(即二次积分)来实现的。 一、利用直角坐标计算二重积分 我们用几何观点来讨论二重积分 f xyd D ∫∫ (, ) σ 的计算问题。 讨论中,我们假定 f (, ) x y ≥ 0 ; 假定积分区域 D可用不等式 axb x ≤ ≤ ϕ ≤ y ≤ ϕ x 1 2 () ()表示, 其中ϕ1( ) x , ϕ 2( ) x 在[,] a b 上连续。 据二重积分的几何意义可知, f xyd D ∫∫ (, ) σ 的值等于以 D 为底,以曲面 z = f (, ) x y 为顶的曲顶柱体的体积
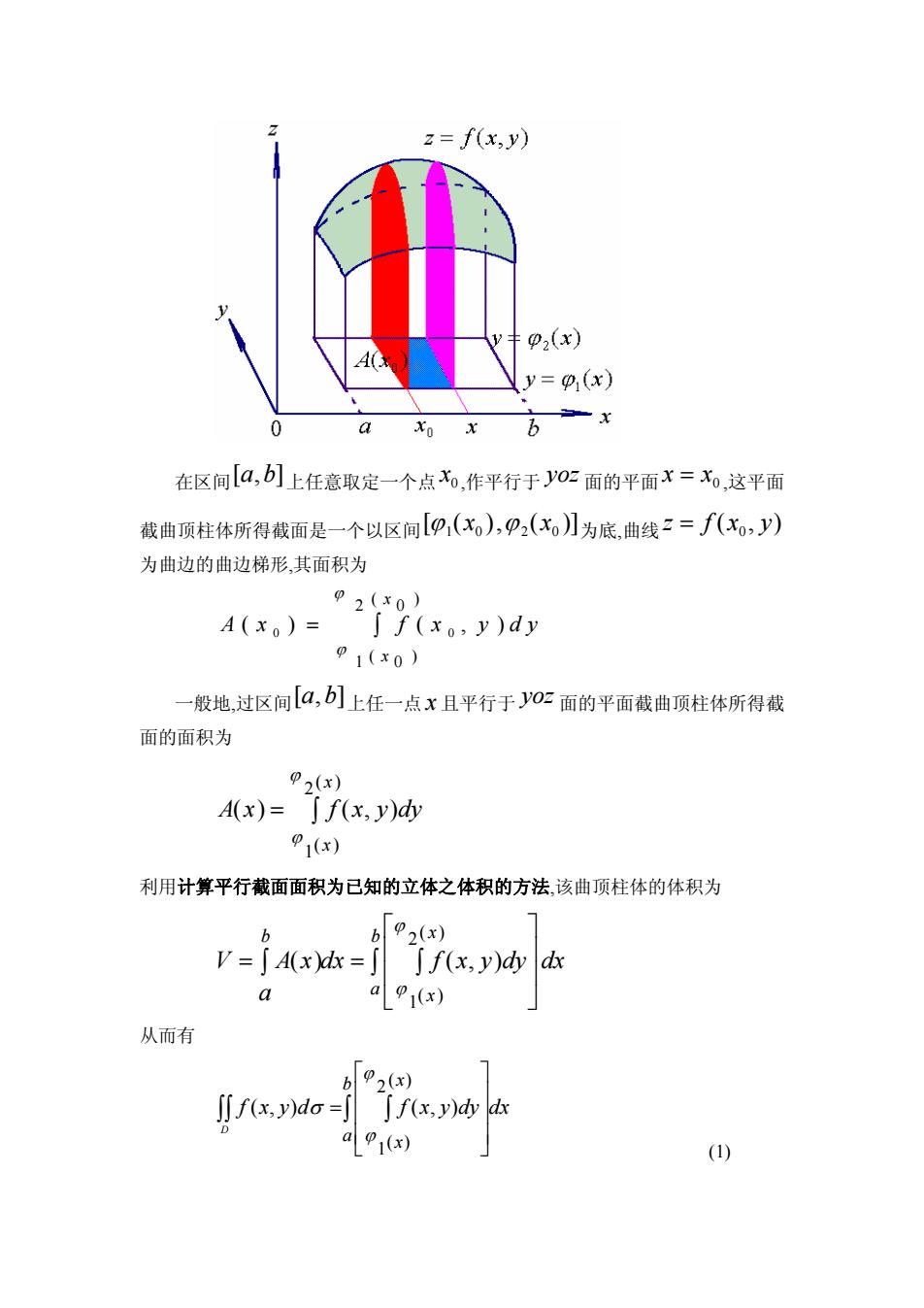
z= f(x,y)92(x)= (@(x)1Ab0axox在区间[α,b]上任意取定一个点o,作平行于yoz面的平面x=xo,这平面截曲顶柱体所得截面是一个以区间[(x),P2(x)为底,曲线z=f(xo,)为曲边的曲边梯形,其面积为P2(x0)A(x。)=J f(xo,y)dy1(xo)一般地,过区间[a,b]上任一点x且平行于yo2面的平面截曲顶柱体所得截面的面积为P2(x)A(x)=J f(x, y)dyPi(x)利用计算平行截面面积为已知的立体之体积的方法,该曲顶柱体的体积为[02(x)bJ f(x, y)dy dxV = A(x)dx =Jaa;(x)从而有[2(t)J f(x, y)do =[J f(x, y)dy dx71a (x)(1)
在区间[,] a b 上任意取定一个点 x0 ,作平行于 yoz 面的平面 x x = 0 ,这平面 截曲顶柱体所得截面是一个以区间[ ( ), ( )] ϕ10 20 x x ϕ 为底,曲线 z = f ( ,) x y 0 为曲边的曲边梯形,其面积为 A x f x y dy x x ( ) ( ,) ( ) ( ) 0 0 1 0 2 0 = ∫ ϕ ϕ 一般地,过区间[,] a b 上任一点 x 且平行于 yoz 面的平面截曲顶柱体所得截 面的面积为 A x f x y dy x x () (, ) ( ) ( ) = ∫ ϕ ϕ 1 2 利用计算平行截面面积为已知的立体之体积的方法,该曲顶柱体的体积为 V Ax a dx f x y dy dx b x x a b = = ⎡ ⎣ ⎢ ⎢ ⎤ ⎦ ⎥ ⎥ ∫ ∫ ∫ () (, ) ( ) ( ) ϕ ϕ 1 2 从而有 f x y d f x y dy dx b a x x D ∫∫ ∫ ∫ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = ( ) 2 ( ) 1 ( , ) ( , ) ϕ ϕ σ (1)