复变函数4.利用平行四边形法求复数的和差两个复数的加减法运算与相应的向量的加减法运算一致J215Z1 + Z2L7.1Z1+x+x1Z1-Z2Z.2U
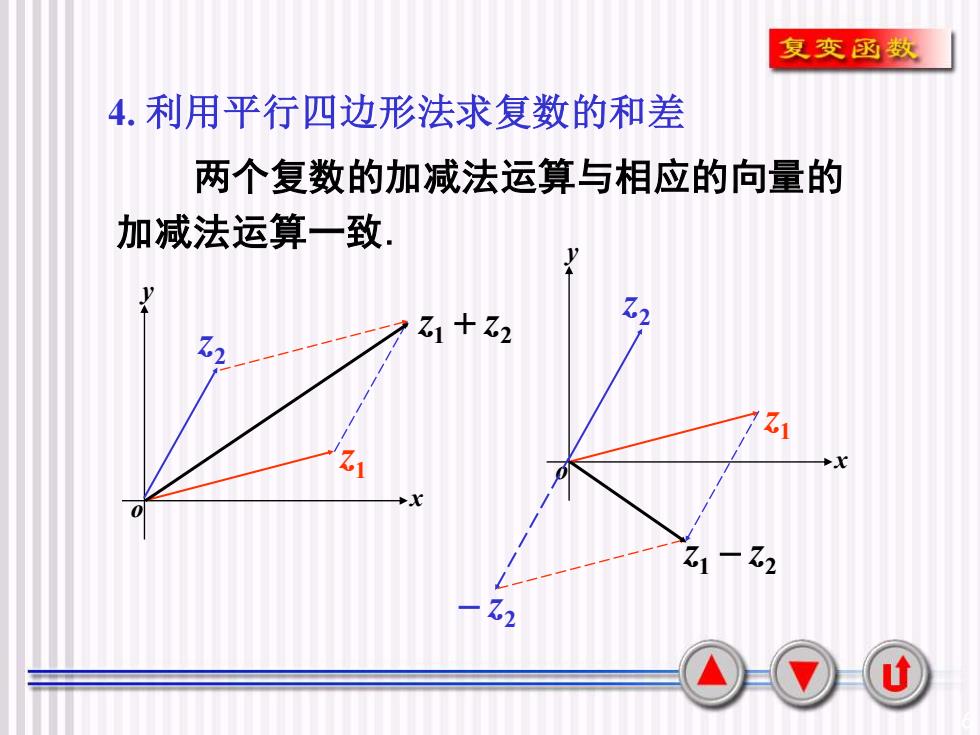
6 4. 利用平行四边形法求复数的和差 x y o 1 z 2 z 1 2 z + z x y o 1 z 2 z 1 2 z − z 2 − z 两个复数的加减法运算与相应的向量的 加减法运算一致
复变函数5.复数和差的模的性质因为2表示点 和 之间的距离,故2Z.2(1) 1 +z2≤+2;Z1 - Z2Z1Z2Z1(2) - 2[≥1-32+x0y一对共轭复数z和z在Iz=x+iy复平面内的位置是关于-x0实轴对称的z=x-iyU
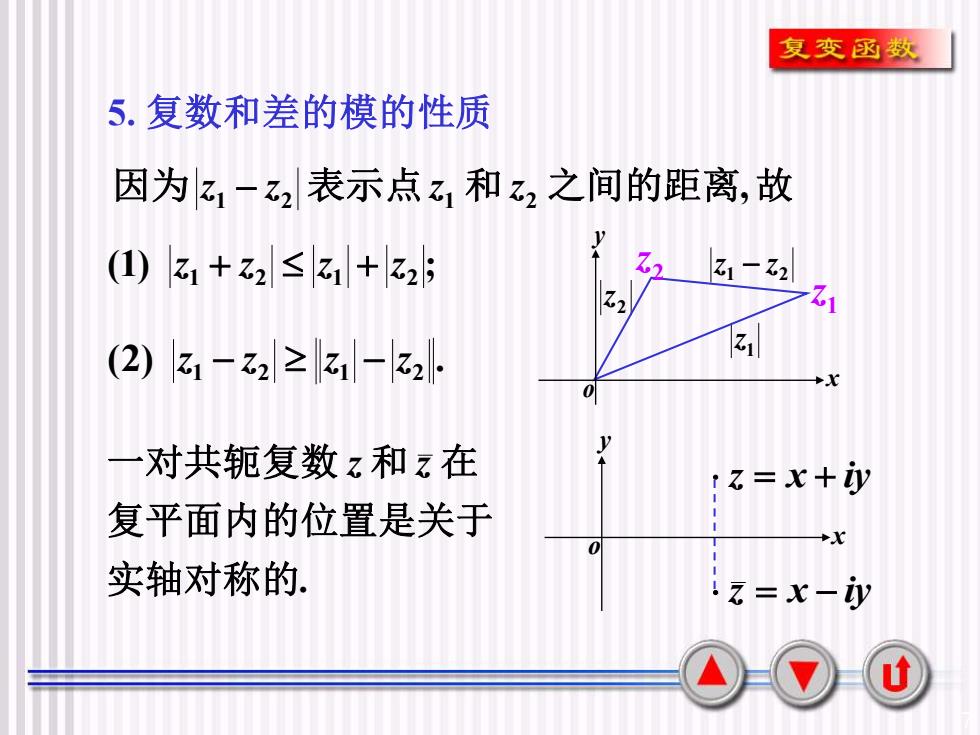
7 5. 复数和差的模的性质 (1) ; 1 2 1 2 z + z z + z (2) . 1 2 1 2 z − z z − z , 因为 z1 − z2 表示点 z1 和 z2 之间的距离 故 1 z 2 z 1 2 z − z x y o 1 z 2 z . 实轴对称的 复平面内的位置是关于 一对共轭复数 z 和 z 在 x y o z = x + iy z = x − iy

复变函数6.复数的三角表示和指数表示x = rcoso.利用直角坐标与极坐标的关系y=rsine,复数可以表示成z=r(cos+isine)复数的三角表示式欧拉介绍再利用欧拉公式eio =cos+isinの,z=reie复数可以表示成复数的指数表示式u
8 利用直角坐标与极坐标的关系 = = sin , cos , y r x r 复数可以表示成 z = r(cos + isin ) 复数的三角表示式 再利用欧拉公式 cos sin , e i i = + 复数可以表示成 i z = re 复数的指数表示式 欧拉介绍 6.复数的三角表示和指数表示

复变函数例1将下列复数化为三角表示式与指数表示式元元(1) z = -~12 - 2i;(2) z = sin I-+icos155(cos5p + isin5)2(3) z :(cos3p-isin3p)3解(1)r=z=/12+4=4,因为z在第三象限V35-2所以θ = arctan元,一元 =arctan元=-菜-36- V12故三角表示式为 =4[cos(-~) isi(1元U
9 例1 将下列复数化为三角表示式与指数表示式: ; 5 cos 5 (1) 12 2 ; (2) sin + z = − − i z = i . (cos 3 sin 3 ) (cos 5 sin5 ) (3) 3 2 i i z − + = 解 (1) r = z = 12 + 4 = 4, 因为z 在第三象限, π 12 2 arctan − − − 所以 = = − 3 3 arctan , 6 5 = − 故三角表示式为 , 6 5 sin 6 5 4 cos + − z = − i

复变函数5指数表示式为z= 4e元元显然r=z=1,(2) z = sin+icos一1553元元元元sin=coscOs一=105523元元元元sinsin=ScOS15三10523元3元”故三角表示式为+ isin=CoS10103元i指数表示式为 z=elo"U
10 指数表示式为 4 . 6 5 i z e − = 5 cos 5 (2) sin + z = i 显然r = z = 1, − = 2 5 cos 5 sin , 10 3 cos = − = 2 5 sin 5 cos , 10 3 sin = 故三角表示式为 , 10 3 sin 10 3 cos + z = i 指数表示式为 . 10 3 i z e =