
第四章线性方程组 二、基础解系及其求法 方程组(4-5)的全部解向量构成个一个向量空 间,称为方程组(4-5)的解空间.它是R”的一个子空 间. 如果方程组(4-5)有非零解由性质4.2.1、4.2.2 知,它一定有无穷多非零解要求出(4-5)的所有解, 只需求出解空间的一个极大线性无关组就行了. 下面我们来求解空间的一个极大线性无关组。 设线性方程组(4-5)系数矩阵A的秩为r,不妨假 设A的前个列向量线性无关,于是A的行最简形为
第四章 线性方程组 二、基础解系及其求法 方程组(4-5)的全部解向量构成个一个向量空 间,称为方程组(4-5)的解空间. 它是R n的一个子空 间. 如果方程组(4-5)有非零解由性质4.2.1、4.2.2 知,它一定有无穷多非零解.要求出(4-5)的所有解, 只需求出解空间的一个极大线性无关组就行了. 下面我们来求解空间的一个极大线性无关组。 设线性方程组(4-5)系数矩阵A的秩为r,不妨假 设A的前r个列向量线性无关,于是A的行最简形为

第四章线性方程组 el 4 0 burt 4 bin 4 4 4 ⅓ %日 eo 4 1 I brr+l h b h 0 0 4 0ú 4 4 4 4 4 4 e ú 0 0 h 0 与对应的线性方程组为 ix =-b水1-4-bn火, 4 (4-7) -K- x=-b4-B
第四章 线性方程组 与I对应的线性方程组为

第四章线性方程组 显然,线性方程组(4-5)与(4-7)同解,在方程 组(4-7)中,给定x+1.Xm一组确定的数,可惟一 确定x1,x,的值,便得到方程组(4-7)的一个解, 也就是方程组(4-5)的一个解,我们把x+1x称 为自由未知量. 令x+1.xn分别取下列1-r组数 ex,+1ùe1ùé0ù e0ù e.úeoúe1ú èx+2i= úei,L 0 e4ú eh'ehú eh4i e ú e ú e ú 昌 ú xniě0iě0
第四章 线性方程组 显然,线性方程组(4-5)与(4-7)同解,在方程 组(4-7)中,给定xr+1,.,xn一组确定的数,可惟一 确定x1 ,.,xr的值,便得到方程组(4-7)的一个解, 也就是方程组(4-5)的一个解,我们把xr+1,.,xn称 为自由未知量. 令xr+1,.,xn分别取下列n-r组数
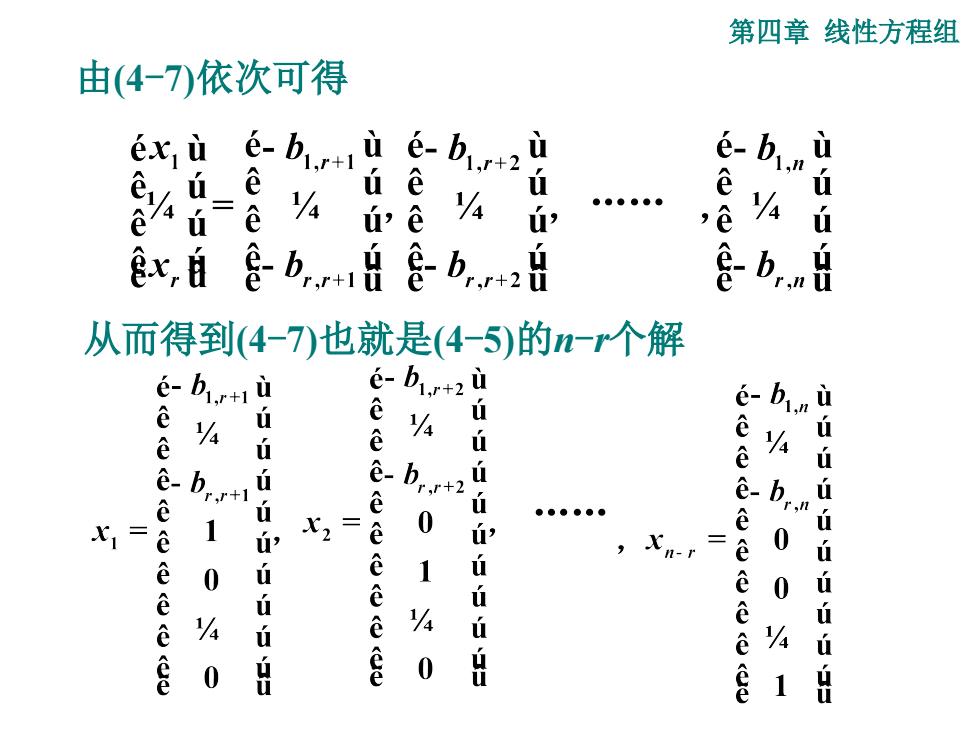
第四章线性方程组 由(4-7)依次可得 xùe-b+1-b+2 e-bi. ùd eú_e úe ú 近 eu=e 4 ú ,e 4 i b 从而得到(4-7)也就是(4-5)的-r个解 b,r+2 6× e 4 方 - b.+2 S5S ●●●●●● 9 1 0 o学 eeeeee 1 2= ú, Xn-r = 0 ú 0 ú 4 ú eeeee 1 i 0 4 i 4 0 9 0 1 H
第四章 线性方程组 由(4-7)依次可得 . 从而得到(4-7)也就是(4-5)的n-r个解