
线性代数第五章 二、二次型的矩阵表示 取ai=aj,则2a,x,=ax,x;+ax,x,(i<j) 于是f=a1x+a22+L+a1wXxm +azx2x+azzx2++aznx2x +L amanamxi =x1(a1k1+a12x2+L+41nXn) +x2(a21X1+2x2+L+42mXn) +L +x (anx+an2x2+L+amx) 版权所有:山东理工大学理学院
线性代数 第五章 版权所有:山东理工大学理学院 二、二次型的矩阵表示 于是

线性代数第五章 a1X1+412X2+L+41nxnù =c,Lx,l8+aa+L+a8 e e M ú e ú a1S1+4n2X2+L+anx éu11 412 422 L úei =x1,X2,L,xn】 a2miè2i eL L L L ue Mi úei ě0ni an2 L Lmiěxni 版权所有:山东理工大学理学院
线性代数 第五章 版权所有:山东理工大学理学院

线性代数第五章 u11 412 L ex1 e ú ú L 记 A= 422 a2nú eL L L X= L e Mu ú eú ě0nl an2 L ěxni 则二次型可记作f=XX,其中A称为二次型的矩阵 显然,A是对称矩阵, 二次型一® 对称矩阵 版权所有:山东理工大学理学院
线性代数 第五章 版权所有:山东理工大学理学院 显然,A是对称矩阵. 二次型 对称矩阵
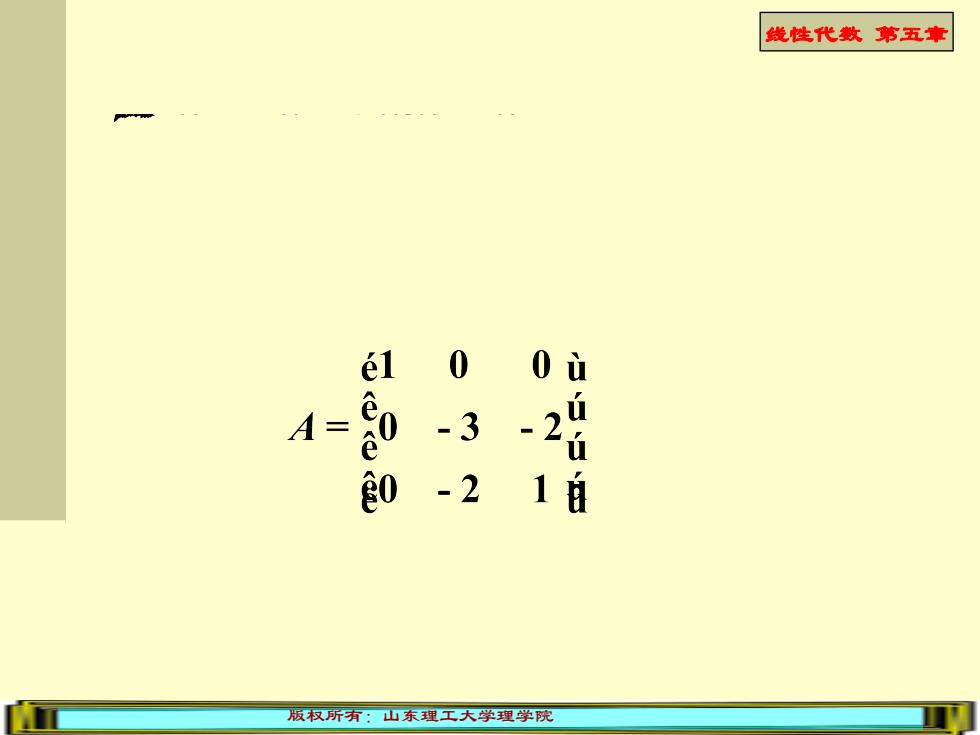
线性代数第五章 el 0 0ù A 3 2 5S 0 -2 版权所有:山东理工大学理学院
线性代数 第五章 版权所有:山东理工大学理学院

线性代数第五章 设由y1,2,4,yn到变量x1,心2,4,x的线性变换为 】x1=C1乃1+C2Jy2+4+C1mJyn, x2=c21y+c222+c2nyn i 444h44 xn=Cmy+Cn2y2++Cmyn" 或写成为矩阵形式:X=CY ex1ù éy1ù e.ú e.ú 其中 X= i Y= e⅓ú =(Cg)n e4ú eú eú ěxni eynù 版权所有:山东理工大学理学院
线性代数 第五章 版权所有:山东理工大学理学院 或写成为矩阵形式: