
线性代数第三章 S3.4分块矩阵 一、分块矩阵的概念 二、分块矩阵的运算 三、分块对角矩阵 上页 下页 返回 版权所有:山东理工大学理学院
线性代数 第三章 版权所有:山东理工大学理学院 一、分块矩阵的概念 二、分块矩阵的运算 三、分块对角矩阵 §3.4 分块矩阵 上页 下页 返回

线性代数第三章 一、分块矩阵的概念 定义设A是一个矩阵,在A的行或列之间加上一些线,把这 个矩阵分成若干小块。用这种方法被分成若干小块的矩阵 叫做一个分块矩阵每一小块称为4的子块,每一个分块的 方法叫做A一种分法 e011a12a13 a14a15ù e」 例如 A= 122 023 24: 025ú 。 132: 33034: a3s e 042:043 a44:4s0 则A可记作 éA 1A2A3ù A= A品 版权所有:山东理工大学理学院
线性代数 第三章 版权所有:山东理工大学理学院 一、分块矩阵的概念 定义 设A是一个矩阵,在A的行或列之间加上一些线,把这 个矩阵分成若干小块.用这种方法被分成若干小块的矩阵 叫做一个分块矩阵.每一小块称为A的子块,每一个分块的 方法叫做A一种分法. 例如 则A可记作
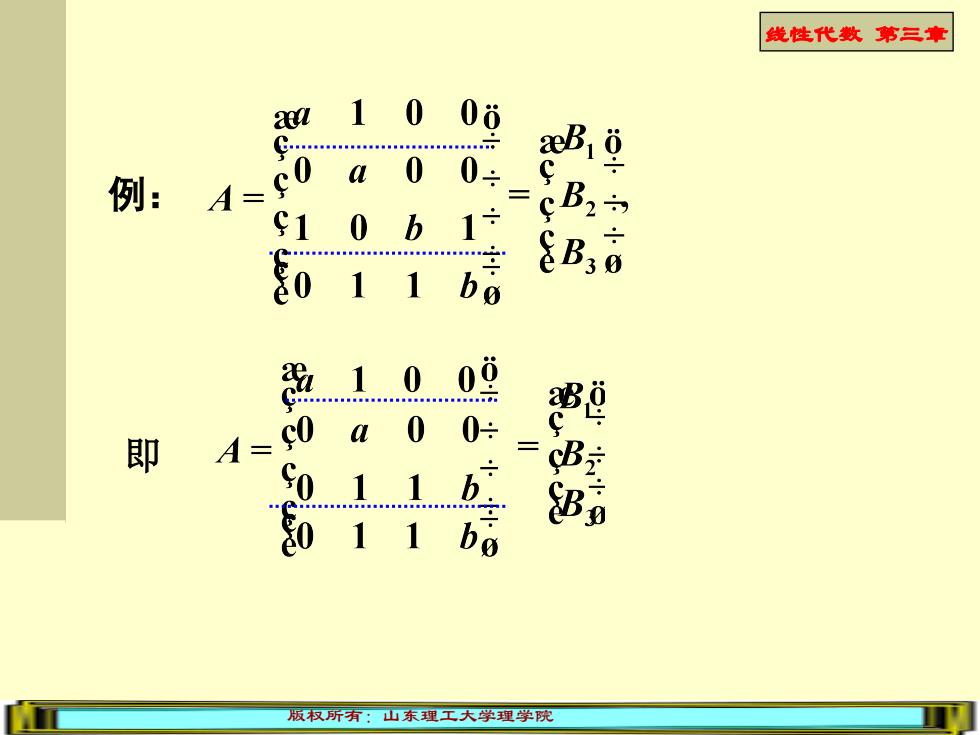
线性代数第三章 28 210 06 2eB16 0 例: 0: A= so a S1 0 b 1 2÷ 011 8B bo 1000 0i8 0: 即 A= c0 a0 011b B 8011 B可 bo 版权所有:山东理工大学理学院
线性代数 第三章 版权所有:山东理工大学理学院 例: 即
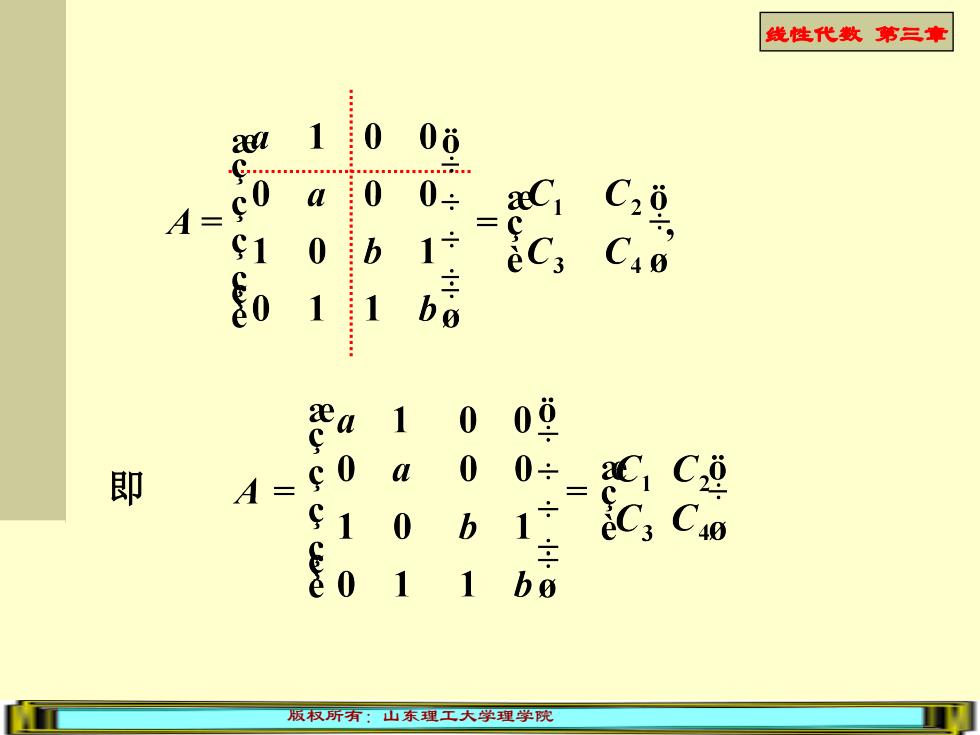
线性代数第三章 . a 1 : 0 06 a 0 0÷ A= C20 C1 0 : b 0 1 1 be 1 0 S 09 即 0 0 0÷ A= C8 0 b 0 1 信 c 版权所有:山东理工大学理学院
线性代数 第三章 版权所有:山东理工大学理学院 即

线性代数第三章 280 1 0 06 0 0片 A 0 其中a g 0 : b E Bo o 1 bo 2e0 0 06 a : 0 0 A ÷ 0 =(444A其中4 b 0 1 1 ÷÷④ 版权所有:山东理工大学理学院
线性代数 第三章 版权所有:山东理工大学理学院