
线性代数第四章 第四章 线性方程组 。S4.1线性方程组的解的判别 ●S4.2齐次线性方程组的解的结构 ●§4.3非齐次线性方程组解的结构 上页 下页 返回 版权所有:山东理工大学理学院
线性代数 第四章 版权所有:山东理工大学理学院 第四章 线性方程组 §4.2 齐次线性方程组的解的结构 §4.1 线性方程组的解的判别 §4.3 非齐次线性方程组解的结构 上页 下页 返回

线性代数第四章 §4.1线性方程组的解的判别 n元线性方程组 i411x1+a12x2+L+41nxn=b1 az+a22x2+L+aznx=b2 (4-1) LLLLLLLLL am+am4mn=bm 记 012 L ain bù e L ǘ L22 2nú A=64 422 L A= b2 eL L L Lú eL L L L ú ě0ml m2 mn ěml L 系数矩阵 增广矩阵 版权所有:山东理工大学理学院
线性代数 第四章 版权所有:山东理工大学理学院 n 元线性方程组 记 §4.1 线性方程组的解的判别 系数矩阵 增广矩阵

线性代数第四章 ex1ù eb,ù eú e ú x= èr2i b= e e Mu e Mu eú e.u exn ěbmi 于是,这个非齐次方程组可以记为 Ax=b (4-2) 由第二章的讨论可知,方程组(4-1)与增广矩阵具有一一对 应关系,对方程组进行加减消元相当于对其增广矩阵进行初等 变换,因此求解方程组的问题就可以转化为矩阵的初等行变化 问题.一般线性方程组的解可能会出现三种情况: 有唯一解、有无穷多解或无解. 版权所有:山东理工大学理学院
线性代数 第四章 版权所有:山东理工大学理学院 Ax = b 于是,这个非齐次方程组可以记为 由第二章的讨论可知,方程组(4-1)与增广矩阵具有一一对 应关系,对方程组进行加减消元相当于对其增广矩阵进行初等 变换,因此求解方程组的问题就可以转化为矩阵的初等行变化 问题.一般线性方程组的解可能会出现三种情况: 有唯一解、有无穷多解或无解 . (4 — 2)

线性代数第四章 一、线性方程组解的判别 定理4.1.1线性方程组: iax+a2x2+L+ainx=b 4+0z,+L+an,=b, LLLLLLLLL (4-1) amdm22amnn=bm 有解的充分必要条件是它的系数矩阵A与增广矩阵A有相同的秩, 即R(A)=R(A) 版权所有:山东理工大学理学院
线性代数 第四章 版权所有:山东理工大学理学院 一、线性方程组解的判别
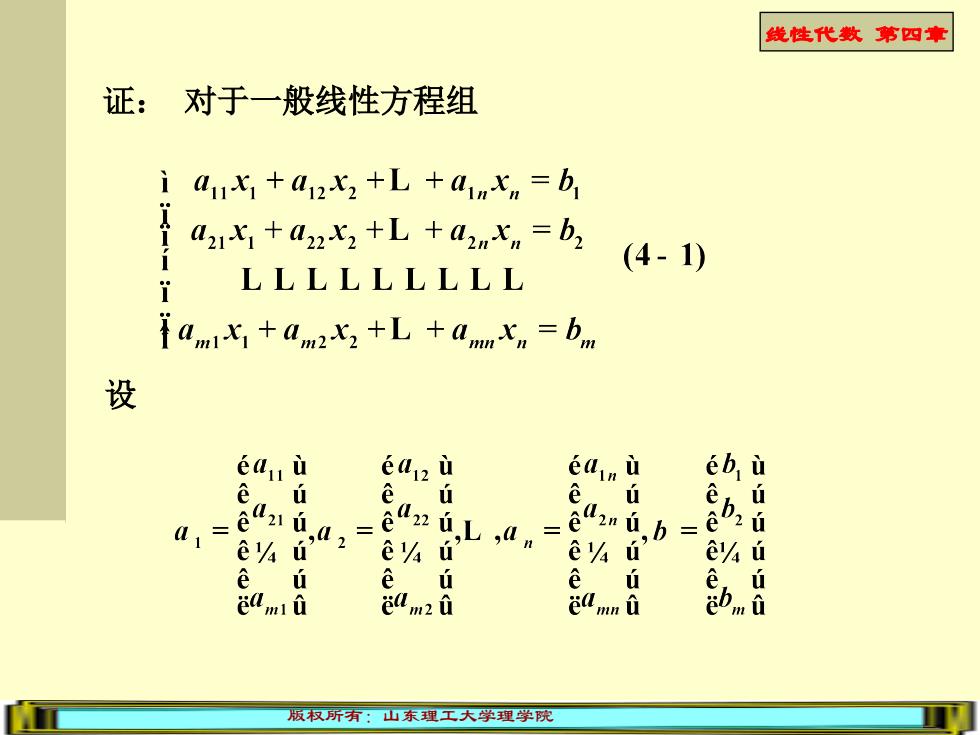
线性代数第四章 证:对于一般线性方程组 i anx+azx2++aunx=b a2+azx2+L+anx=b2 (4-1) LLLLLLLLL amx+am2x2+amnxn=bm 设 eauu e412ù eainu ebù eú eú eú 621úa,=L,0m= è42mi,b= e4ú eu e4ú eu eú eú eú e,ú edm edm2 ěLmni m 版权所有:山东理工大学理学院
线性代数 第四章 版权所有:山东理工大学理学院 证: 对于一般线性方程组 设