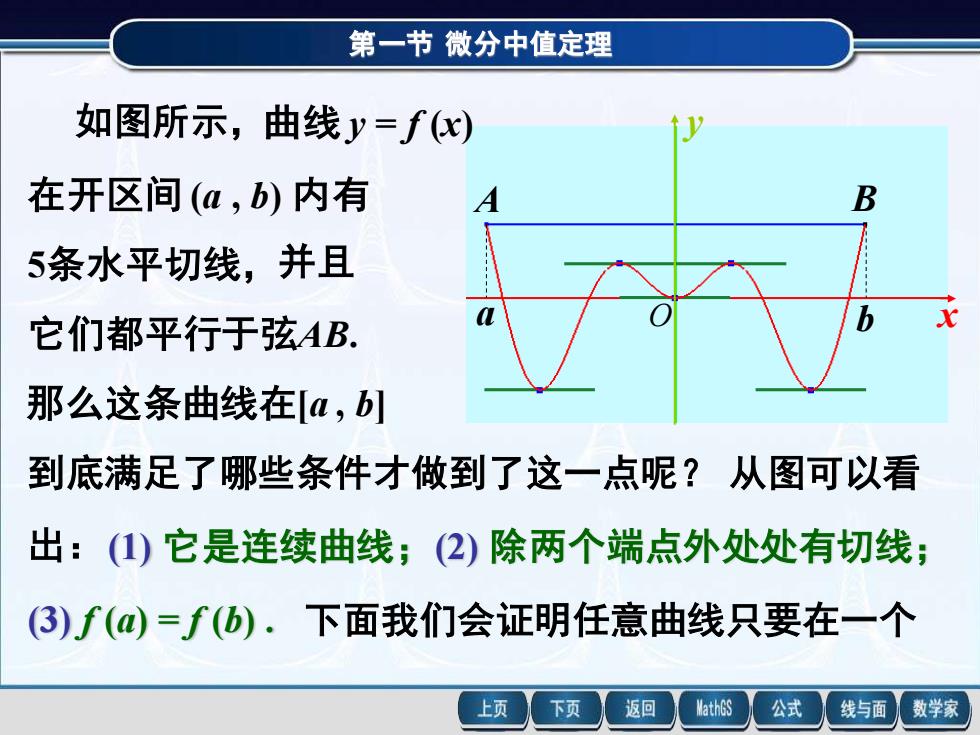
第一节微分中值定理 如图所示,曲线y=f(x) 在开区间(a,b)内有 D 5条水平切线,并且 它们都平行于弦AB. 那么这条曲线在a,b] 到底满足了哪些条件才做到了这一点呢?从图可以看 出:()它是连续曲线;(2)除两个端点外处处有切线; (3)f(@)=f(b).下面我们会证明任意曲线只要在一个 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 微分中值定理 a b A B x y O 如图所示,曲线 y = f (x) 在开区间 (a , b) 内有 5条水平切线,并且 它们都平行于弦AB. 那么这条曲线在[a , b] 到底满足了哪些条件才做到了这一点呢? 从图可以看 出:(1) 它是连续曲线;(2) 除两个端点外处处有切线; (3) f (a) = f (b) . 下面我们会证明任意曲线只要在一个

第一节微分中值定理 (1)它是连续曲线;(2)除两个端点外处处有切线; (3)f(@=f(b). 闭区间上满足上述三个条件,则在相应的开区间内一定 有水平切线 把上述用几何语言描述的条件和结论用分析语言描 述出来就是下面的罗尔定理 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 微分中值定理 (1) 它是连续曲线;(2) 除两个端点外处处有切线; (3) f (a) = f (b) . 闭区间上满足上述三个条件,则在相应的开区间内一定 有水平切线. 把上述用几何语言描述的条件和结论用分析语言描 述出来就是下面的罗尔定理