
©少东罪工大军 2a+c=1, a=0, 2b+d=0, b=-1, → -a=0, → c=1, -b=1, d=2. 又因为 AB BA 02020-0 所以 r=0 上页
− = − = + = + = 1, 0, 2 0, 2 1, b a b d a c = = = − = 2. 1, 1, 0, d c b a 又因为 − 1 0 2 1 − 1 2 0 1 − 1 0 2 1 = − 1 2 0 1 , 0 1 1 0 = 所以 . 1 2 0 1 1 − = − A AB BA

©卢东承工大军 2、利用公式 a 12 伴随矩阵:设A 21 a22 a2n an an2 ann A 4 An 则,A= A2 A如 An2 是A的伴随矩阵。 An A2n 其中A是,的代数余子式。 回
2、利用公式 伴随矩阵: 设 11 12 1 21 22 2 1 2 n n n n nn a a a a a a A a a a = 11 21 1 12 22 2 1 2 n n n n nn A A A A A A A A A A = 则, 是A的伴随矩阵。 其中Aij是 aij 的代数余子式

©少本用2大军 定理1矩阵A可逆的充要条件是A≠0,且 其中A*为矩阵A的伴随矩阵 证明必要性若A可逆,即有A使AA=E. 故AA=E=1,所以A≠0. 上页
定理1 矩阵 可逆的充要条件是 ,且 , −1 1 = A A A A A 0 证明 若 A 可逆, A AA = E. 即有 −1使 −1 1, 1 = = − 故 A A E 所以A 0. 其中A 为矩阵A的伴随矩阵. 必要性
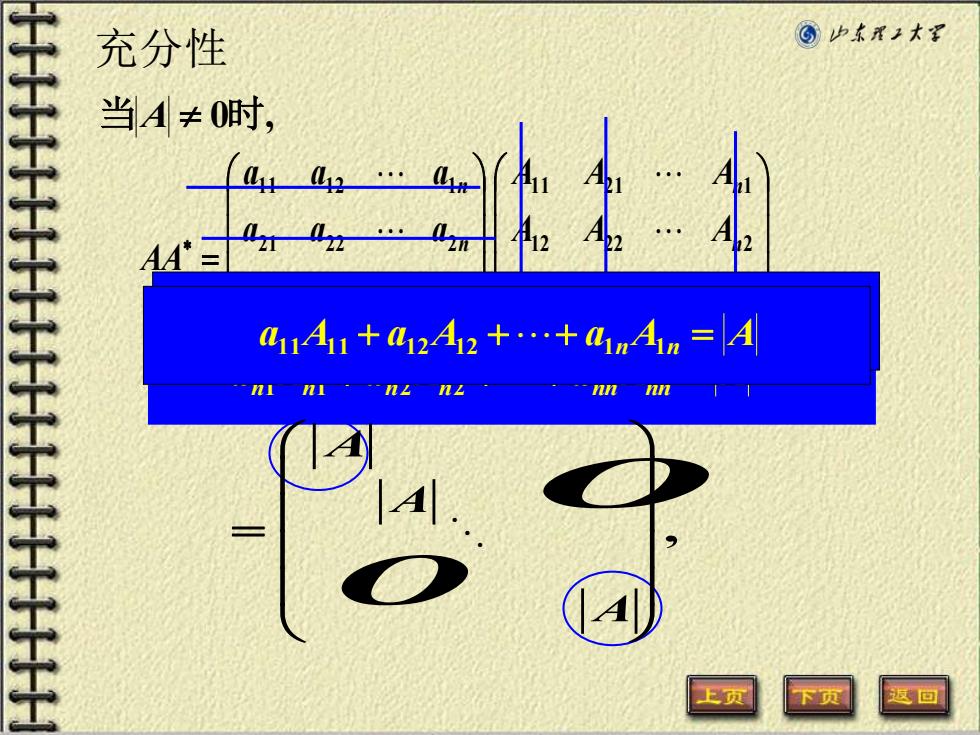
充分性 ⑤P东承上大军 当A≠0时, 41A11+4242+.+4mAn=A nnnn 上页 区回
当A 0时, = n n nn n n n n nn n n A A A A A A A A A a a a a a a a a a AA 1 2 1 2 2 2 2 1 1 2 1 1 1 2 2 1 2 2 2 1 1 1 2 1 an1An1 + an2An2 ++ annAnn = A , A = O O 充分性 A 21 21 22 22 2 2 n n a A a A a A A + + + = A a11A11 + a12A12 ++ a1nA1n = A

©少东罪工大军 AM=AA=AE÷AA 4=E, A 按逆矩阵的定义得 证毕 A 奇异矩阵与非奇异矩阵的定义 当A=0时,A称为奇异矩阵当A≠0时,A称为 非奇异矩阵 由此可得4是可逆阵的充要条件是4为非奇异矩阵 王
AA = A A = AE A E, A A A A A = = . 1 A A A − = 按逆矩阵的定义得 证毕 . 0 , , 0 , 非奇异矩阵 当A = 时 A称为奇异矩阵当A 时 A称 为 奇异矩阵与非奇异矩阵的定义 由此可得A是可逆阵的充要条件是A为非奇异矩阵