
第二章 随机变量及其分布 第一节 随机变量 随机变量的引入 二、随机变量的概念
二、随机变量的概念 一、随机变量的引入 第一节 随机变量 第二章 随机变量及其分布

随机变量的引入 1.为什么引入随机变量? 概率论是从数量上来研究随机现象内在规律 性的,为了更方便有力地研究随机现象,就要用 数学分析的方法来研究,因此为了便于数学上的 推导和计算,就需将任意的随机事件数量化.当 把一些非数量表示的随机事件用数字来表示时, 就建立起了随机变量的概念
概率论是从数量上来研究随机现象内在规律 性的,为了更方便有力地研究随机现象,就要用 数学分析的方法来研究, 因此为了便于数学上的 推导和计算,就需将任意的随机事件数量化.当 把一些非数量表示的随机事件用数字来表示时, 就建立起了随机变量的概念. 1. 为什么引入随机变量? 一、随机变量的引入
2.随机变量的引入 实例1抛掷骰子,观察出现的点数. 则有 S-{1,2,3,4,5,6}样本点本身就是数量 X(e)=e 恒等变换 X(1)=1,X(2)=2,X3)=3,X(4)=4,X(⑤)=5,X(6)=6, 且有 PIX-1-6 (i=1,2,3,4,5,6)
实例1 抛掷骰子,观察出现的点数. X(1) = 1, X(2) = 2, X(3) = 3, X(4) = 4, X(5) = 5, X(6) = 6, , ( 1,2,3,4,5,6). 6 1 P{X = i} = i = S={1,2,3,4,5,6} 样本点本身就是数量 恒等变换 且有 X(e) = e 则有 2. 随机变量的引入

{X≤4}表示事件掷出的点数小于4点 42 P{X>2}= 6 3 实例2:一批出厂电视,随意抽取一台,用Y表示这 台电视的寿命. {Y≤4000(单位:小时)表示事件电视寿命不大于 4000小时
{ 4} X 表示事件掷出的点数小于4点 4 2 { 2} 6 3 P X = = 实例2:一批出厂电视,随意抽取一台,用Y表示这 台电视的寿命. { 4000}( ) Y 单位:小时 表示事件电视寿命不大于 4000小时
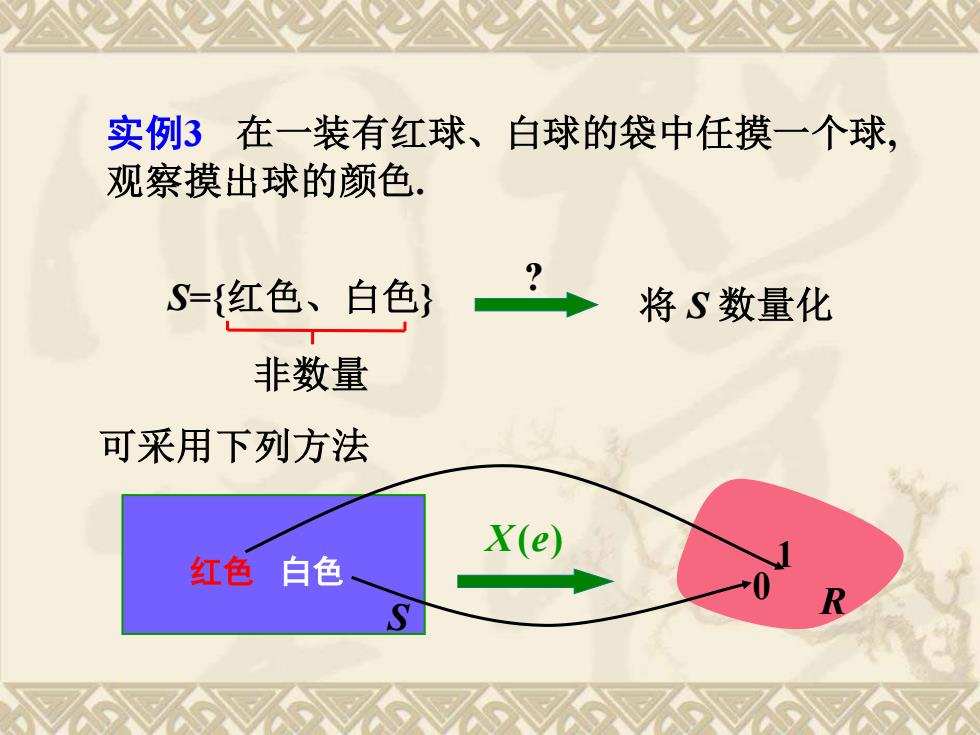
实例3在一装有红球、白球的袋中任摸一个球, 观察摸出球的颜色. S={红色、白色} 将S数量化 非数量 可采用下列方法 X(e) 红色 白色
实例3 在一装有红球、白球的袋中任摸一个球, 观察摸出球的颜色. S={红色、白色} 非数量 将 S 数量化 ? 可采用下列方法 S 红色 白色 X(e) R 1 0