《复变函数与积分变换》课程教学资源（PPT课件）第五章 留数及其应用 5.3 第三节 留数在定积分计算上的应用

复变函数(z2-1)°dza-Va?-b?Ii-- 2i2"b z --a + a2 -67bb(-a+ Va2-b)= 2元 i Res[f(z),0]+ Res f(z),b2元 Va2 - b22a元62b22元(a- Va2 -b2)u

6 2 2 2 2 2 π 2π b a b b a − = − ( ). 2 2 2 2 a a b b − −  =  =         − − − −         − + − − − − = 1 2 2 2 2 2 2 2 2 ( 1) d z b a a b z b a a b iz b z z z               − + − = + b a a b i f z f z ( ) 2π Res ( ),0 Res ( ), 2 2

复变函数dxMT计算(a > 0).例2J0a + sin'xdxdx元元解11- cos2xJoJOa + sin'xa+2d2x令 2x=t,二一2J01 - cos2xa+21dzdt2元0二1-(z2 + 1)/2zi记22 Jo1-cost[z]=1 a+a+22dz2i0=2- 2(2a + 1)z +1z=1U

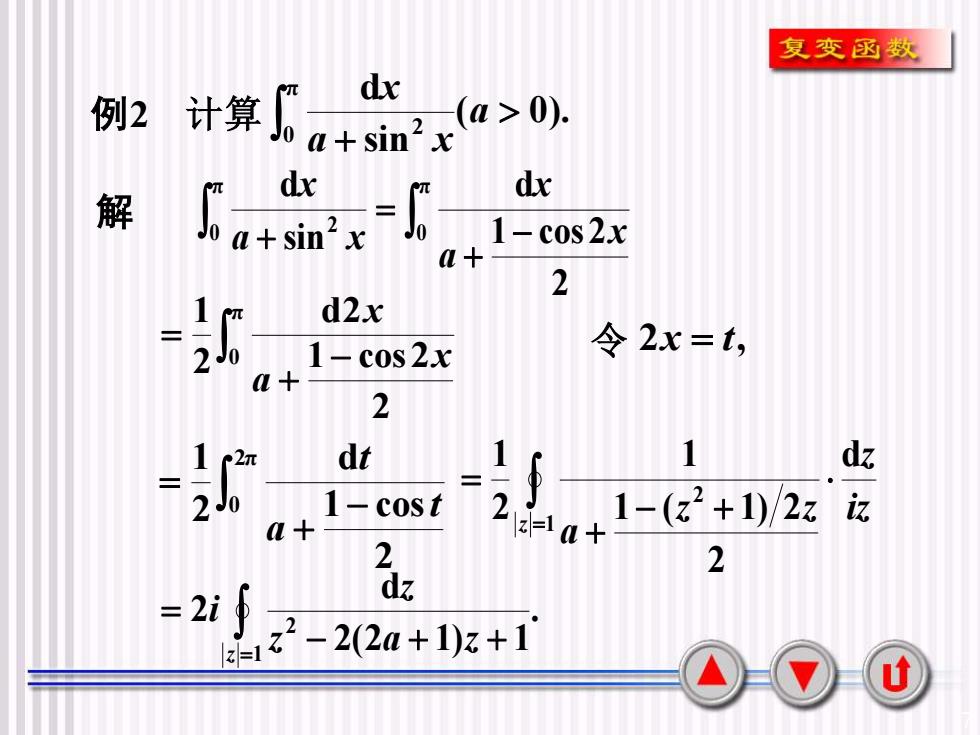
7 例2 计算 ( 0). sin π d 0 2  +  a a x x 解   − + = + π 0 π 0 2 2 1 cos 2 d sin d x a x a x x  − + = π 0 2 1 cos 2 d2 2 1 x a x 令 2x = t,  − + = 2π 0 2 1 cos d 2 1 t a t iz z z z a z d 2 1 ( 1) 2 1 2 1 1 2  − + + =  = . 2(2 1) 1 d 2 1  2 = − + + = z z a z z i

复变函数极点为：z=2a+1-/(2a+1)2-1(在单位圆内)z2=2a+1+V(2a+1)2-1 (在单位圆外)dx元所以JOa +sin'x= 2元 i. 2iRes[f(z),(2a + 1 - V(2a +1)2 -1)2元-/(2a + 1)2 -1u

8 2 1 (2 1) 1 2 极点为 : z1 = a + − a + −  + π 0 2 sin d a x x 所以 . (2 1) 1 2π 2 + − = a (在单位圆内) 2 1 (2 1) 1 2 z2 = a + + a + − (在单位圆外) 2π 2 Res[ ( ),(2 1 (2 1) 1)]. 2 = i  i f z a + − a + −

复变函数cOs20?2元例3计算 / - 1-2p00 0 p 1)的值.解由于0<p<1,1-2pcos + p2 =(1 - p)2 + 2p(1 - cos)在0≤9≤2元内不为零，故积分有意义(e2i0 + e-2i0)0) =(2 + z),由于 cs2O =二(2I = f 2'+2?1dz2izZ+Z[z|=11-2p+p2U

9 例3 d (0 1) . 1 2 cos 2π cos2 0 计算 2   的值 − + =  p p p I    解 由于0  p  1, 1 2 cos (1 ) 2 (1 cos ) 2 2 − p  + p = − p + p −  在0    2π内不为零， 故积分有意义. ( ) 2 1 cos 2 2  2   i i e e − 由于 = + ( ), 2 1 2 −2 = z + z iz z p z z p z z I z d 2 1 2 1 2 2 1 1 2 2  + + −   + = − = − 

复变函数dz1+z7=-1iz2Z+ ZCz=11-2p+p241+ z4dz = ff(z)dz.02iz(1- pz)(z - p)[z=1[z|-11被积函数的三个极点z=0,P,二pz=0,p,在圆周z=1内,且z=0为二级极点，z=p为一级极点，u

10 iz z p z z p z z I z d 2 1 2 1 2 2 1 1 2 2  + + −   + = − = −  z iz pz z p z z d 2 (1 )( ) 1 1 2 4  = − − + = , 1 0, , p 被积函数的三个极点z = p z = 0, p,在圆周z = 1内， 且z = 0为二级极点，z = p为一级极点， ( )d . 1 f z z z  = =