
第19讲洛朗级数 洛朗级数 洛朗级数的应用 ·洛朗级数与泰勒级数 lexu@mail.xidian.edu.cn 矩阵论●
lexu@mail.xidian.edu.cn 矩阵论 6 第19讲 洛朗级数 洛朗级数 洛朗级数的应用 洛朗级数与泰勒级数

洛朗级数 冬在以z为圆心的圆域内解析的函数fa可以在圆域内 展开成(z-z)的幂级数 若fz在z不解析,如何将函数展开成(a-z)的级数? ·研究解析函数在孤立奇点领域内的性质 ·是定义留数以及计算留数的必要基础 ·在许多应用中,往往需要将在z不解析,但在z去心领域 内解析的函数展开成级数 洛朗级数 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩阵论 7 洛朗级数 在以z0为圆心的圆域内解析的函数f(z)可以在圆域内 展开成(z-z0)的幂级数 若f(z)在z0不解析,如何将函数展开成(z-z0)的级数? 研究解析函数在孤立奇点领域内的性质 是定义留数以及计算留数的必要基础 在许多应用中,往往需要将在z0不解析,但在z0去心领域 内解析的函数展开成级数 洛朗级数
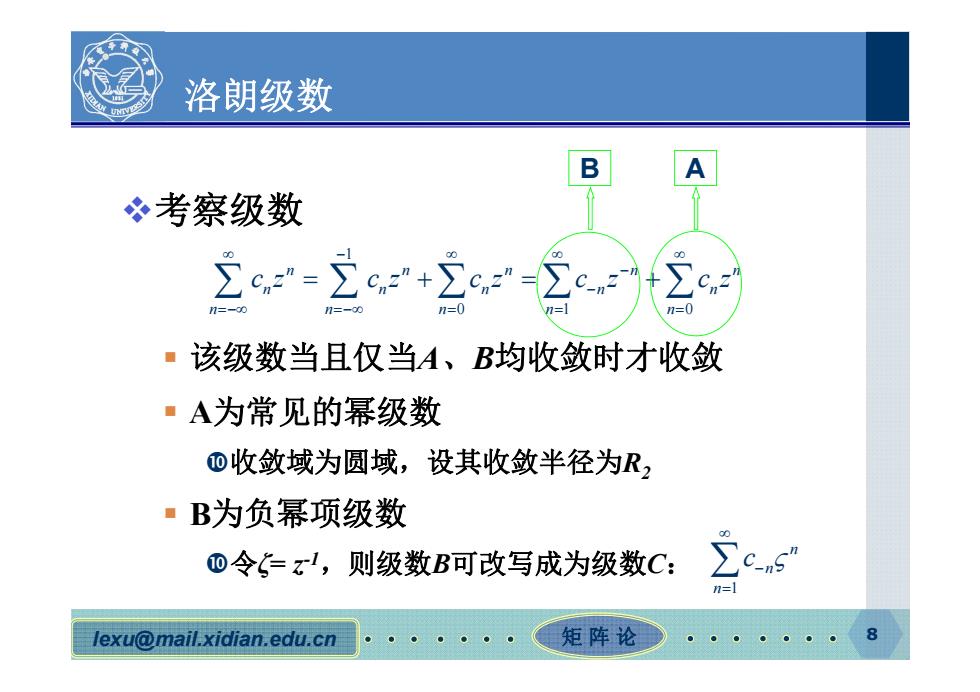
洛朗级数 B 考察级数 2c-2c ·该级数当且仅当A、B均收敛时才收敛 ·A为常见的幂级数 o收敛域为圆域,设其收敛半径为R, ■B为负幂项级数 0令=x,则级数B可改写成为级数C: c5 =1 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩阵论 8 洛朗级数 考察级数 该级数当且仅当A、B均收敛时才收敛 A为常见的幂级数 收敛域为圆域,设其收敛半径为R2 B为负幂项级数 令ζ= z-1,则级数B可改写成为级数C: 1 01 0 n nn nn n nn n n n n nn n cz cz cz c z cz B A 1 n n n c

洛朗级数 n=1 ·C为常见的正幂项级数 D收敛域为圆域,设其收敛半径为R,即I<R时级数 C收敛 o即当Ik<R时,级数B收敛 ·令R=1R,则有 z|>R B收敛 A收敛 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩阵论 9 洛朗级数 C为常见的正幂项级数 收敛域为圆域,设其收敛半径为R,即|ζ|<R时级数 C收敛 即当 |1/z |<R 时,级数B收敛 令R1=1/R ,则有 1 n n n c C |z |> R1 |z |< R2 A收敛 B收敛
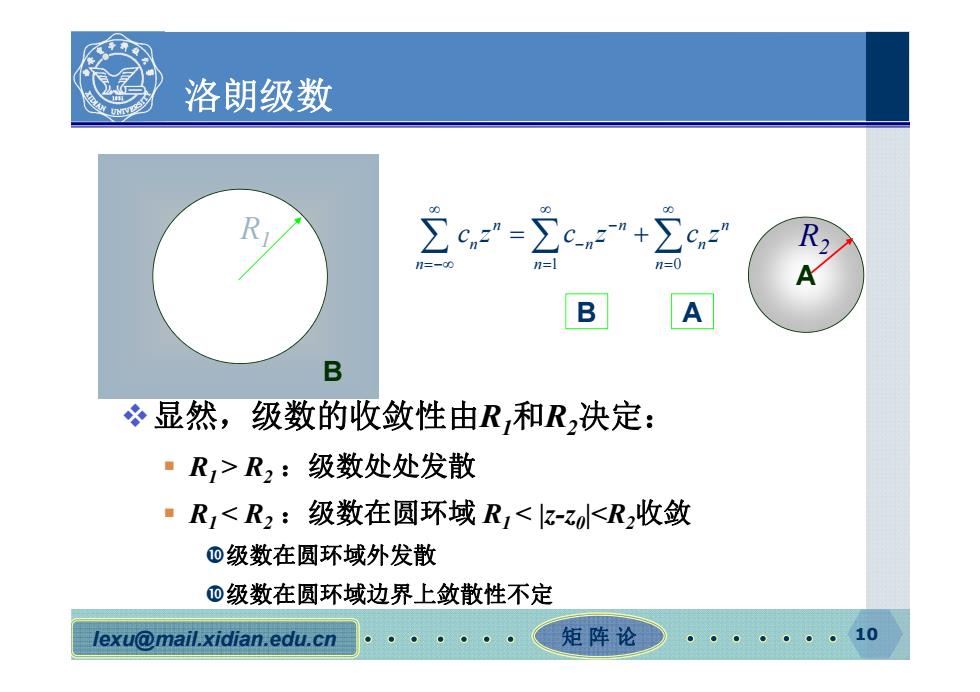
洛朗级数 立c=c+ n=0 B B 显然,级数的收敛性由R和R,决定: ·R>R2:级数处处发散 ·R,<R2:级数在圆环域R1<a-z<R2收敛 ⑩级数在圆环域外发散 D级数在圆环域边界上敛散性不定 lexu@mail.xidian.edu.cn 矩阵论 10
lexu@mail.xidian.edu.cn 矩阵论 10 洛朗级数 显然,级数的收敛性由R1和R2决定: R1 > R2 :级数处处发散 R1 < R2 :级数在圆环域 R1 < |z-z0|<R2收敛 级数在圆环域外发散 级数在圆环域边界上敛散性不定 B R1 A R2 1 0 n nn n nn nn n cz c z cz B A