
例1 y= x3 ,求(1)dy, (2)dylx=2 (3) dyx=24x=0.02解 '= 3x2(1) dy = (x3)4x = 3x2△x= 3x24x =124x(2) dylx=2x=23x4x= 0.24.(3)dyx=2C=24x=0.024x=0.02
例 1 解 3 2 , (1)d , (2)d , x y x y y = = 求 2 y x = 3 0.02 d 2 (3) ==xx y = 0.24. 0.02 2 2 0.02 (3)d 2 3 == == = xx x y x x x (1) dy (x ) x 3 = = x x 2 3 = = = = y x x x x 2 2 2 (2) d 3 12x
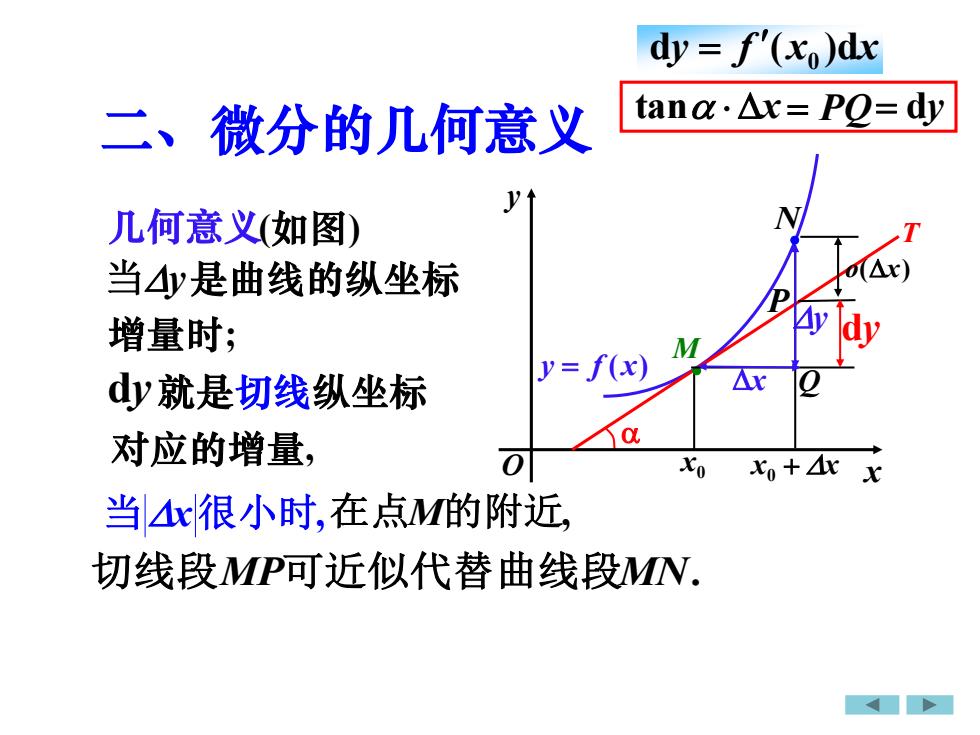
dy = f'(x,)dxtanα·△x= PO= dy微分的几何意义二、ytN几何意义(如图)T0(△x)当4y是曲线的纵坐标PAydy增量时;My= f(x)Ax0dy就是切线纵坐标α对应的增量可XoXo + 4xx当4x很小时,在点M的附近切线段MP可近似代替曲线段MN
几何意义 当y 当x很小时, (如图) dy dy = f (x0 )dx 二、微分的几何意义 对应的增量, 切线段MP可近似代替曲线段MN. 增量时; 是曲线的纵坐标 在点M的附近, 就是切线纵坐标 tan x = PQ= dy x y O y = f (x) T x0 M• x0 + x N • P Q y dy o(x) x