
泰勒(Taylor)(英)1685-1731第三节泰勒(Taylor)公式泰勒公式的建立1儿个初等函数的麦克劳林公式近似计算与误差估计1其它应用小结思考题泰勒,B
泰勒(Taylor)(英)1685-1731 第三节 泰勒(Taylor)公式 ◼ 泰勒公式的建立 ◼ 几个初等函数的麦克劳林公式 ◼ 近似计算与误差估计 ◼ 其它应用 ◼ 小结 思考题

泰勒公式的建立多项式函数简单的,熟悉的函数来近似代替复杂函数理论分析用多项式近似表示函数一应用近似计算特点(1)易计算函数值(2)导数与积分仍为多项式;(3)多项式由它的系数完全确定,而其系数文由它在一点的函数值及导数值确定用怎样的多项式去逼近给定的函数误差又如何呢
简单的, 多项式函数 特点 (1)易计算函数值; (2)导数与积分仍为多项式; (3)多项式由它的系数完全确定, 又由它在一点的函数值及导数值确定. 而其系数 用怎样的多项式去逼近给定的函数 误差又如何呢 一、泰勒公式的建立 熟悉的函数来近似代替复杂函数. 用多项式近似表示函数 — 应用 理论分析 近似计算

回想微分若f"(x)存在,在x,附近有f(xo +△r)-f(xo) ~ f'(x.)r记x = x, +△x一次多项式f(x) ~ (f(xo)+ f'(x.)(x-x)f(x) =f(xo)+ f'(xo)(x- xo)+ o(x -xo)当x一→x,时,其误差是比x一x)高阶的无穷小
f (x) = ( ) , 若f x0 存在 记 x = x0 + x f (x0 + x) − f (x0 ) f (x0 )x 回想微分 在x0 附近有 ( ) ( ) ( )( ) 0 x0 x x0 f x f x + f − , 当x → x0 时 ( ) . 其误差是比 x − x0 高阶的无穷小 一次多项式 ( ) ( )( ) 0 0 0 f x + f x x − x ( ) + o x − x0
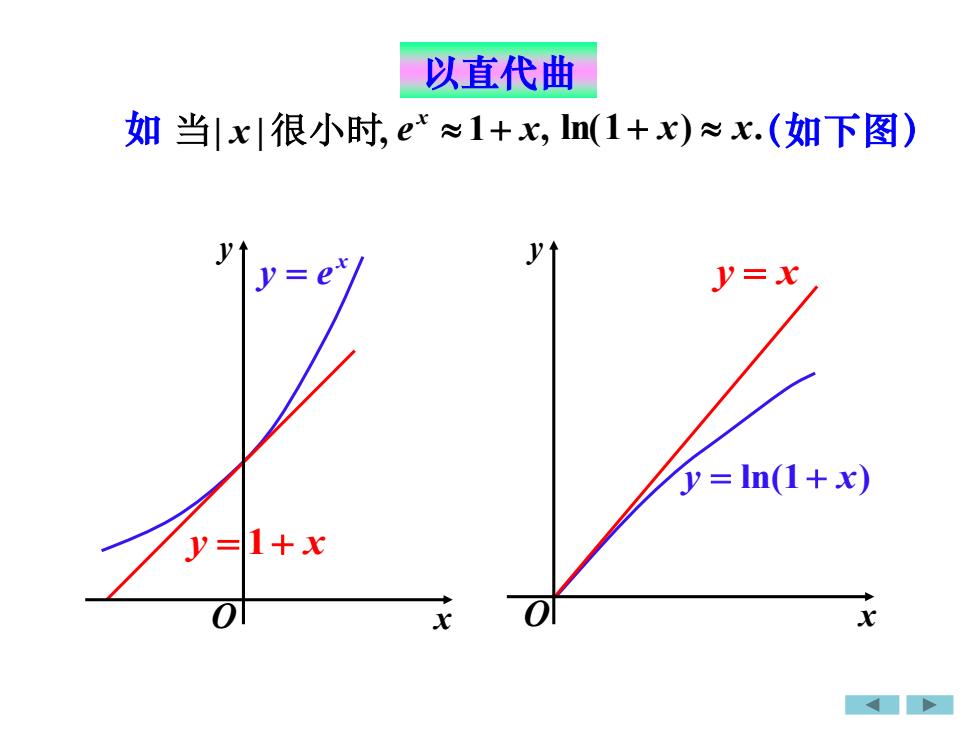
以直代曲如 当|x|很小时,e*~1+x,ln(1+x)~x.(如下图)y=xy = In(1 + x)y=1+xoofxx
y = 1 + x x y = e y = x y = ln( 1 + x ) 如 当| x |很小时, e x 1+ x, ln(1+ x) x (如下图) . 以直代曲 x y x O yO

一次多项式f(xo)+ f'(x)(x-x) ~ f(x)不足1.精确度不高;2.误差不能定量的估计希望不在x,附近用适当的高次多项式@x-x)+P,(x)=@+@(x-xo)+@(x-x)"二1()问题(1)系数怎么定?(2)误差(如何估计)表达式是什么?
需要解决的问题 如何提高精度 ? 如何估计误差 ? 问题 (1) 系数怎么定? (2) 误差(如何估计)表达式是什么? 不足 1. 精确度不高;2. 误差不能定量的估计. ( ) ( )( ) 0 x0 x x0 f x + f − f (x) 希望 f (x) 一次多项式 在x0附近 用适当的高次多项式 n n n a x x P x a a x x a x x ( ) ( ) ( ) ( ) 0 2 0 1 0 2 0 + − = + − + − + L