《高等数学》课程教学资源（PPT课件）第二章 导数与微分 2-05 第五节 函数的微分

2.微分的定义定义设函数y= f(x)在某区间内有定义x,及x,+△xr在这区间内如果A为微分系数A△x + o(Ax)Ay = f(xo + △x)- f(xo) =成立(其中A是与△x无关的常数,则称函数y=f(x)在点x,可微，并称A·△x为函数y=f(x)在点x,相应于自变量增量△x的微分，记作dy|x=x,或df(xo),即dy| =x, = A·Ax

2. 微分的定义 定义 设函数y = f (x)在某区间内有定义, , x0 及 x0 + x在这区间内 y = f (x0 + x) − f (x0 ) = 如果 成立(其中A是与x无关的常数), 0 y = f (x)在点x 则称函数 A x 0 d x x y = y = f (x)在点x0相应于自变量 d . 0 y A x 即 x= x =   可微, d ( ), x0 或 f 微分, 记作 并称 为函数 增量x的 A为微分系数 Ax + o(x)

满足什么条件的函数是可微的呢？3.微分的系数A如何确定呢？定在x)微分与导数有何关系呢？下面的定理回答了这些问题dy=f'(x)Ax证(1)必要性：f(x)在点x,可微:. Ay = A . △x + o(△x),Ayo(△x:. lim4limA+ArAr-→0 LAxAr→0即函数f(x)在点x,可导,且A= f'(x)

3. 可微的充分必要条件 定理 函数 f (x)在点x0 可微 证 (1) 必要性 ( ) ,  f x 在点x0可微 y = A x + o(x),  = A. ( ) , 即函数 f x 在点x0 可导 函数 f (x) d ( ) . y = f  x0 x 即有 ( ). x0 且A = f   , 在点x0处可导 ( ), 0 且 A = f  x =   x y x o x A   + ( ) 0 lim x→   0 lim x→ 满足什么条件的函数是可微的呢？ 微分的系数A如何确定呢? 微分与导数有何关系呢? 下面的定理回答了这些问题

定理函数f(x)在点x,可微台/函数f(x)在点x处可导,且A=f(x),即有dy=f(x)△x(2)充分性:函数f(x)在点x,可导AyAy= f'(x),:. Jim即= f'(x,)+α,Ar-→>0 △xAr(r →0, α→0)从而 4y = f'(x)· 4x +α· (4x)= f'(x). Axr + o(Ax),:函数f(x)在点x,可微,且f(xo)= A.:.可导台可微.其微分一定是dy =f(x)x求导法又叫微分法

(2) 充分性 ( ) ( ), y = f  x0  x +  x ( ) , =  0 +    f x x y 即 ( ) , 函数f x 在点x0可导 lim ( ), 0 0 f x x y x =      → ( ) ( ), = f  x0  x + o x ( ) , 函数 f x 在点x0可微 可导 可微. 求导法又叫微分法 d ( ) . 0 y = f  x x 从而 ( ) . 且 f  x0 = A  其微分一定是 定理 函数 f (x)在点x0 可微 函数 f (x) 即有  , 在点x0处可导 ( ), 0 且 A = f  x d ( ) . y = f  x0 x (x →0, →0)

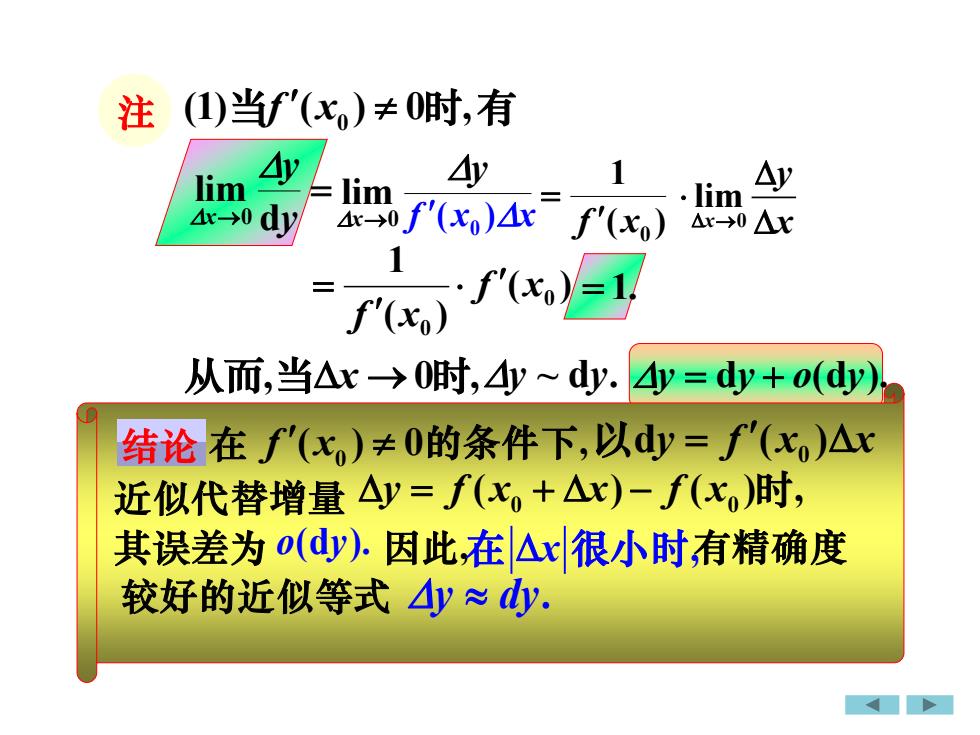
注(1)当f(x)≠0时,有y4y7Aylimlimlim4x=0 f'(xo)4x4x-→0dyf'(xo)Ar→0 Ax1=1(xof'(xo)从而,当△x 一→0时,4y ～ dy.Ay = dy + o(dy)结论在f（x）±0的条件下，以dy=f（x）A近似代替增量 Ay= f(x。+△r)-f(x,)时,其误差为o(dy).因此在△x很小时有精确度较好的近似等式4y～dy

注 = → y y x d lim 0   ( ) 1 x0 f  = 0 (1) ( ) 0 , 当f x   时 有   = ( ) 1 x0 f 从而, 0 , 当 →x 时 即dy y 是 的 ( 0). 当 →x 微分的实质 y x   0 lim → ( ) x0 f  = 1. y = dy + o(dy). d ( )0 又由于 y f x x x =    是 的 y ~ dy. 线性函数, 线性主部. f ( x )x 0  0 lim x y  → x    主部, 称dy y 是 的 所以在 条件下, 0 f x ( ) 0  在 的条件下, d ( )0 以 y f x x =   0 0 近似代替增量  = +  − y f x x f x ( ) ( ) , 时 其误差为 o(dy). 因此, 在 x 很小时, 有精确度 较好的近似等式 y  dy. 结论 0 f x ( ) 0 

注(2)函数y=f(x)在任意点x处的微分，称为函数的微分，记作dy 或 df(x),即dy = f'(x)4x与x和4x有关(3)通常把自变量x的增量4x称为自变量的微分，记作dx，即dx=4x.dy:. dy = f'(x)dx→f'(x)dx导数又称为微商

与x和x有关 (3)通常把自变量x的增量x dy = f (x)dx ( ) d d f x x y =  导数又称为微商 称为函数 的微分, 记作dy 或 df (x)， 即dy = f (x)x. 称为自变量的 微分,记作 dx, 即dx = x. 注 （2）函数y =f (x)在任意点x处的微分