
例1设随机变量X具有分布密度kx,0≤x<3f(x)=32-x/2,3≤x≤4其它[0,(2) 求P(1< X ≤,(1) 确定常数k;;(3)分布函数F(x)。1解 (l)令1=f f(x)dx=['kxdx+(2-=)dx91-k+得k=426·71241(2) P(1<X≤号}=]T(2dxxdx?48216
− = 0, 其 它 2 / 2, 3 4 , 0 3 ( ) x x kx x f x 解 − (1) 令1 = f (x)d x 设随机变量X具有分布密度 确定常数 求 };(3)分布函数 ( )。 2 7 (1) k; (2) P{1 X F x 例1 x x kx x )d 2 d (2 3 0 4 3 = + − 6 1 得 k = 4 1 2 9 = k + } 2 7 (2) P{1 X 48 41 = = + − 7/ 2 3 3 1 )d 2 d (2 6 1 x x x x

0x人02x0≤x人312(3) F(x) =f(x)dx :2r+2x-33<x人44x≥4福课后:画X分布函数图形来验证F(x)的性质
− − + − = = x x x x x x x x F x f x d x 1 4 2 3 3 4 4 0 3 12 0 0 (3) ( ) ( ) 2 2 课后:画X分布函数图形来验证F(x)的性质

三.常用的连续型随机变量的分布均匀分布设随机变量X具有概率密度1a<x<bf(x)=3 b-a其它0,则称服从区间(a,b)上的均匀分布,记作X~U(a,b)图形:b
均匀分布 设随机变量X 具有概率密度 = − 0, 其 它 , 1 ( ) a x b f x b a 则称X服从区间(a,b)上的均匀分布, 记作 X ~ U(a,b) O x f ( x) • a • b ( ) 1 b − a 三.常用的连续型随机变量的分布 图形:
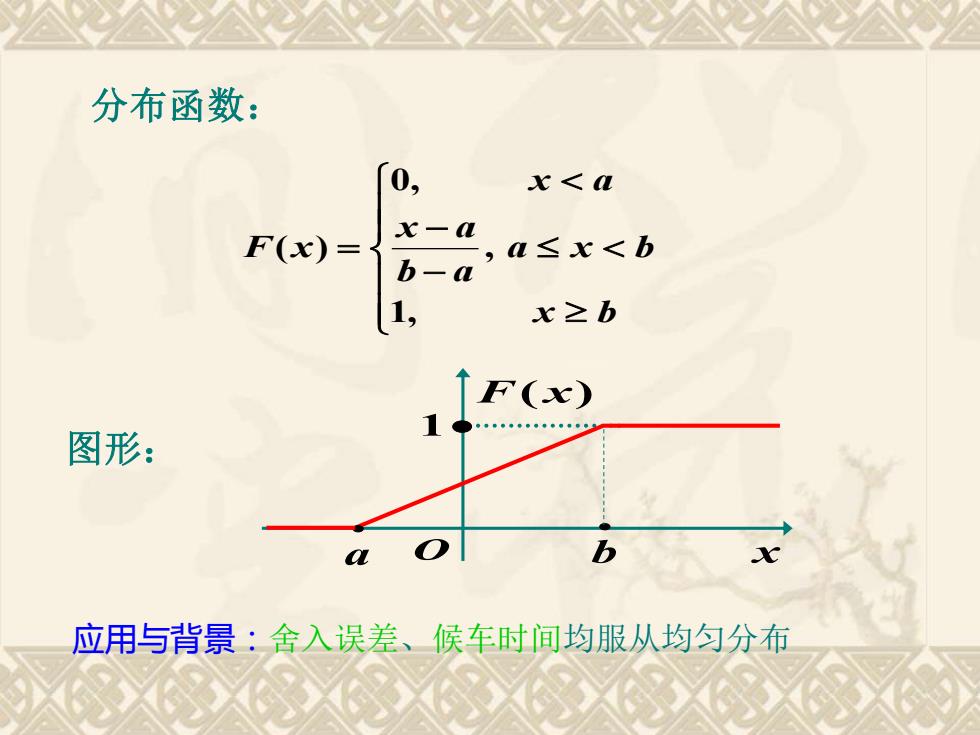
分布函数:0,x<axaF(x) =a≤x<bb-a1x≥bF(x)图形:b应用与背景:舍入误差,候车时间均服从均匀分布
− − = x b a x b b a x a x a F x 1, , 0, ( ) O x F(x) • a • b 1• 应用与背景:舍入误差、候车时间均服从均匀分布 分布函数: 图形: