
导航 =2- 9 c 20 P 1 c%=20 故X的分布列为 X 0 1 2 3 1 9 9 1 P 20 20
导航 P(X=2)= 𝐂𝟑 𝟐 𝐂𝟑 𝟏 𝐂𝟔 𝟑 = 𝟗 𝟐𝟎 , P(X=3)= 𝐂𝟑 𝟑 𝐂𝟑 𝟎 𝐂𝟔 𝟑 = 𝟏 𝟐𝟎 . 故 X 的分布列为 X 0 1 2 3 P 𝟏 𝟐𝟎 𝟗 𝟐𝟎 𝟗 𝟐𝟎 𝟏 𝟐𝟎
导航 延伸探究 1例1的条件不变,若记取出白球的个数为1,求,的分布列. 解:由题意可知,1的取值范围为{0,1,故1服从两点分布.因为 Pr=号=所以刀的分布列为 1 0 1 1 1 P 2 2
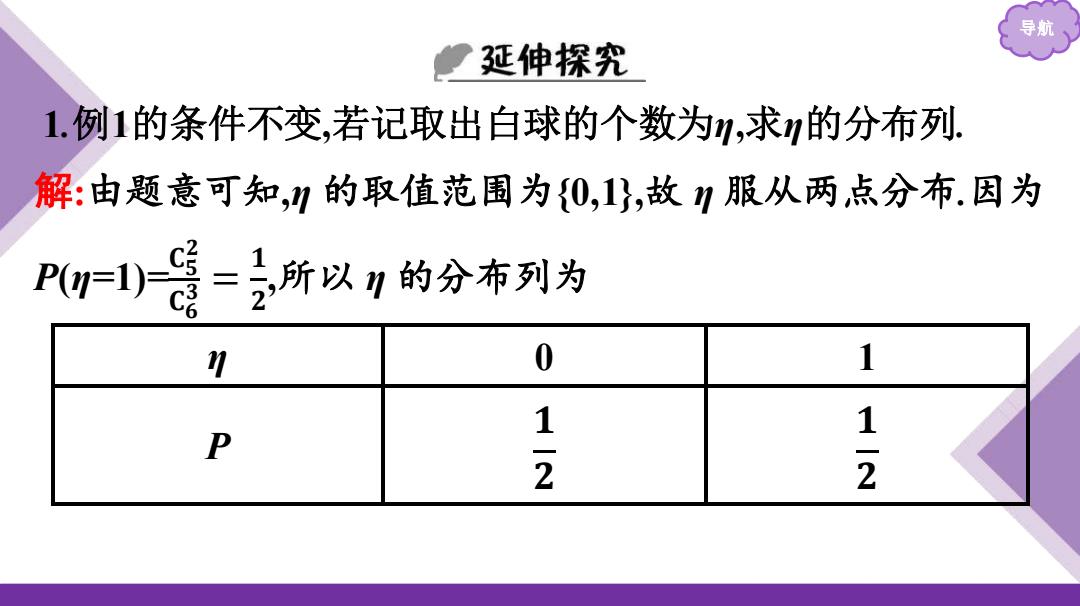
导航 1.例1的条件不变,若记取出白球的个数为η,求η的分布列. 解:由题意可知,η 的取值范围为{0,1},故 η 服从两点分布.因为 P(η=1)= 𝐂𝟓 𝟐 𝐂𝟔 𝟑 = 𝟏 𝟐 ,所以 η 的分布列为 η 0 1 P 𝟏 𝟐 𝟏 𝟐

导 2.把例1的条件“一次随机取出3个球”改为“有放回地抽取3次, 每次取出1个球”,其他条件不变,结果又如何? 解:(山)由题意可知,任取1个球,取出红球的概率为取出黑球 的概率为,取出白球的概率为,故取出的3个球颜色都不相 同的率PA×××名
导航 2.把例1的条件“一次随机取出3个球”改为“有放回地抽取3次, 每次取出1个球”,其他条件不变,结果又如何? 解:(1)由题意可知,任取 1 个球,取出红球的概率为𝟏 𝟐 ,取出黑球 的概率为𝟏 𝟑 ,取出白球的概率为𝟏 𝟔 ,故取出的 3 个球颜色都不相 同的概率 P=𝐀𝟑 𝟑 × 𝟏 𝟐 × 𝟏 𝟑 × 𝟏 𝟔 = 𝟏 𝟔

2)由题意可知,任取1个球,取出编号为1的球的概率为2 故XB(3,) 故Px0-Cg×((x() 1-8 P(X-I)-C3xix() 38 Px2-c3×(x 38
导航 (2)由题意可知,任取 1 个球,取出编号为 1 的球的概率为𝟏 𝟐 , 故 X~B 𝟑, 𝟏 𝟐 . 故 P(X=0)=𝐂𝟑 𝟎 × 𝟏 𝟐 𝟎 × 𝟏 𝟐 𝟑 = 𝟏 𝟖 , P(X=1)=𝐂𝟑 𝟏 × 𝟏 𝟐 × 𝟏 𝟐 𝟐 = 𝟑 𝟖 , P(X=2)=𝐂𝟑 𝟐 × 𝟏 𝟐 𝟐 × 𝟏 𝟐 = 𝟑 𝟖