导航 特别地,如果X~HN,n,0且n+M-N≤0,则X能取所有不大于s的 自然数,此时X的分布列如下表所示 X 0 1 ●●● k S P CMCN-M CMCN-M CMCNM C囧 囧 ●… C囧
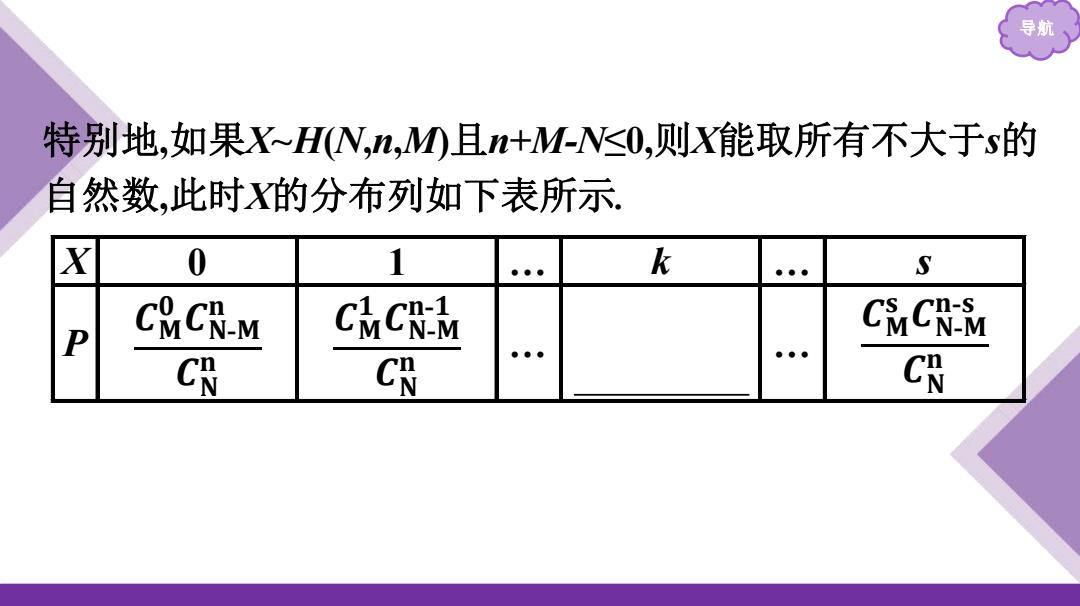
导航 特别地,如果X~H(N,n,M)且n+M-N≤0,则X能取所有不大于s的 自然数,此时X的分布列如下表所示. X 0 1 … k … s P 𝑪𝐌 𝟎 𝑪𝐍-𝐌 𝐧 𝑪𝐍 𝐧 𝑪𝐌 𝟏 𝑪𝐍-𝐌 𝐧-𝟏 𝑪𝐍 𝐧 … 𝑪𝐌 𝐤 𝑪𝐍-𝐌 𝐧-𝐤 𝑪𝐍 𝐧 … 𝑪𝐌 𝐬 𝑪𝐍-𝐌 𝐧-𝐬 𝑪𝐍 𝐧

导月 3.做一做:已知从4名男生和2名女生中任选3人参加数学竞赛, 则所选3人中,女生不超过1人的概率为 答案 解析:设所选女生的人数为X,则XH(6,3,2), 故PO≤I=PX=0+PK=I)-gs 4
导航 3.做一做:已知从4名男生和2名女生中任选3人参加数学竞赛, 则所选3人中,女生不超过1人的概率为 . 答案: 𝟒 𝟓 解析:设所选女生的人数为 X,则 X~H(6,3,2), 故 P(X≤1)=P(X=0)+P(X=1)= 𝐂𝟐 𝟎 𝐂𝟒 𝟑 𝐂𝟔 𝟑 + 𝐂𝟐 𝟏 𝐂𝟒 𝟐 𝐂𝟔 𝟑 = 𝟒 𝟓

导期 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√,错 误的画“X” (1)从4名男演员和3名女演员中选出4人,其中女演员的人数X 服从超几何分布.( (2)袋中有3个白球、4个黑球,每次从中取出1个球,有放回地 取3次,则白球的个数X服从超几何分布.(
导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“×” . (1)从4名男演员和3名女演员中选出4人,其中女演员的人数X 服从超几何分布.( √ ) (2)袋中有3个白球、4个黑球,每次从中取出1个球,有放回地 取3次,则白球的个数X服从超几何分布.( × )

导航 课堂·重难突破 探究一超几何分布 【例1】一个袋中装有6个大小、质地完全相同的小球,其中 红球有3个,编号为1,2,3;黑球有2个,编号为1,2;白球有1个,编 号为1现从袋中一次随机取出3个球 (1)求取出的3个球的颜色都不相同的概率; (2)记取出编号为1的球的个数为X,求X的分布列
导航 课堂·重难突破 探究一 超几何分布 【例1】一个袋中装有6个大小、质地完全相同的小球,其中 红球有3个,编号为1,2,3;黑球有2个,编号为1,2;白球有1个,编 号为1.现从袋中一次随机取出3个球. (1)求取出的3个球的颜色都不相同的概率; (2)记取出编号为1的球的个数为X,求X的分布列

导航 解:(1)从袋中一次随机取出3个球,取法总数为C=20,取出的 3个球的颜色都不相同的取法种数为C3C2C1=6,故取出的3个 球的颜色都不相同的概率为P品0= 10 (2)由题意可知,X~H(6,3,3), 则P(X=0)= c- c昭 20 PX=1)= 9 c 203
导航 解:(1)从袋中一次随机取出 3 个球,取法总数为𝐂𝟔 𝟑 =20,取出的 3个球的颜色都不相同的取法种数为𝐂𝟑 𝟏 𝐂𝟐 𝟏 𝐂𝟏 𝟏 =6,故取出的3个 球的颜色都不相同的概率为 P= 𝟔 𝟐𝟎 = 𝟑 𝟏𝟎 . (2)由题意可知,X~H(6,3,3), 则 P(X=0)= 𝐂𝟑 𝟎 𝐂𝟑 𝟑 𝐂𝟔 𝟑 = 𝟏 𝟐𝟎 , P(X=1)= 𝐂𝟑 𝟏 𝐂𝟑 𝟐 𝐂𝟔 𝟑 = 𝟗 𝟐𝟎