
全程设计 4.2.2 等差数列的前n须和公式 第2课时 等差数列前n项和的应用
4.2.2 等差数列的前n项和公式 第2课时 等差数列前n项和的应用
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随 堂 训 练

导 素养·目标定位 目标素养 L.运用等差数列的前项和知识解决一些实际问题,提升数学 建模核心素养 2.会利用等差数列前项和的函数特征求最值,提升逻辑推理 和数学运算的核心素养 3.能运用裂项相消法解决一些数列求和问题,提升逻辑推理和 数学运算的核心素养
导航 目 标 素 养 1.运用等差数列的前n项和知识解决一些实际问题,提升数学 建模核心素养. 2.会利用等差数列前n项和的函数特征求最值,提升逻辑推理 和数学运算的核心素养. 3.能运用裂项相消法解决一些数列求和问题,提升逻辑推理和 数学运算的核心素养. 素养·目标定位
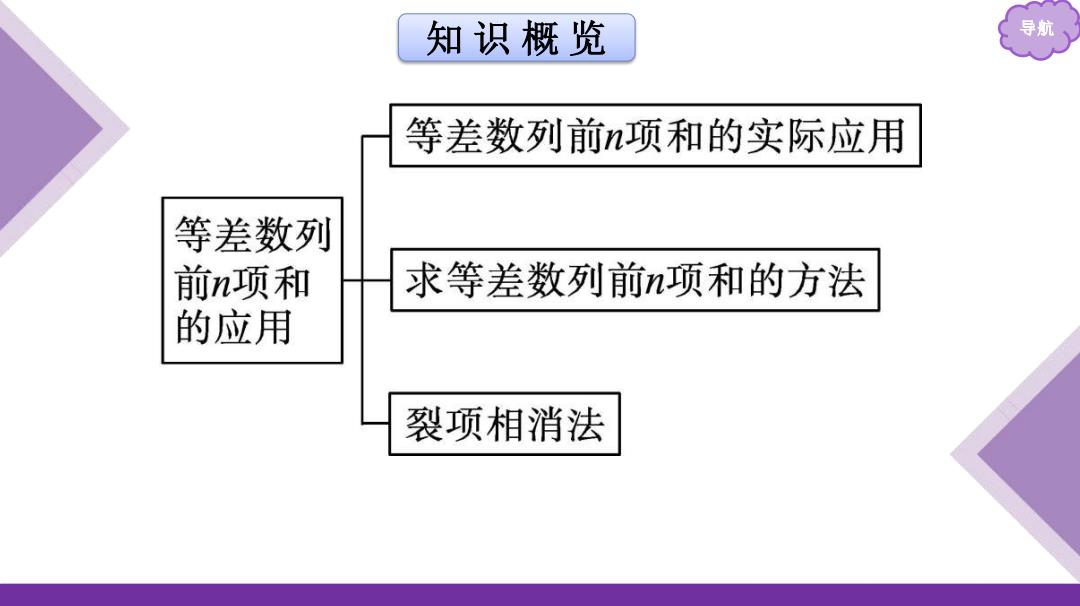
知识概览 导航 等差数列前n项和的实际应用 等差数列 前n项和 求等差数列前n项和的方法 的应用 裂项相消法
知 识 概 览 导航

课前·基础认知 L.等差数列{a,}的前n项和公式的函数特征 等差数列a}的前n项和公式S,=a+可化成关于n的 表达式:S,受2+(a1-)m当40时,Sn关于n的表达式是一个常 数项为零的二次式,即点(n,Sm)在其相应的 函数的图象 上,这就是说等差数列的前n项和公式是关于n的二次函数,它的 图象是抛物线y受+(α1-上横坐标为正整数的一系列孤立 的点
导航 1.等差数列{an }的前n项和公式的函数特征 等差数列{an}的前 n 项和公式 Sn=na1+ 𝒏(𝒏-𝟏)𝒅 𝟐 可化成关于 n 的 表达式:Sn= 𝒅 𝟐 n 2 + 𝒂𝟏- 𝒅 𝟐 n.当 d≠0 时,Sn关于 n 的表达式是一个常 数项为零的二次式,即点(n,Sn)在其相应的 二次 函数的图象 上,这就是说等差数列的前 n 项和公式是关于 n 的二次函数,它的 图象是抛物线 y= 𝒅 𝟐 x 2 + 𝒂𝟏- 𝒅 𝟐 x 上横坐标为正整数的一系列孤立 的点. 课前·基础认知