
全程设计 4.3.1 等比数列的概念 第2课时 等比数列的性质
4.3.1 等比数列的概念 第2课时 等比数列的性质
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随 堂 训 练

导 素养.目标定位 目标素养 1.掌握等比数列的性质及其应用通过等比数列性质的学习, 提升逻辑推理素养 2.熟练掌握等比数列与等差数列的综合应用,提升数学运算素 养 3.能够熟练应用等比数列知识解决生活中的实际问题,提升数 学建模素养
导航 目 标 素 养 1.掌握等比数列的性质及其应用.通过等比数列性质的学习, 提升逻辑推理素养. 2.熟练掌握等比数列与等差数列的综合应用,提升数学运算素 养. 3.能够熟练应用等比数列知识解决生活中的实际问题,提升数 学建模素养. 素养·目标定位
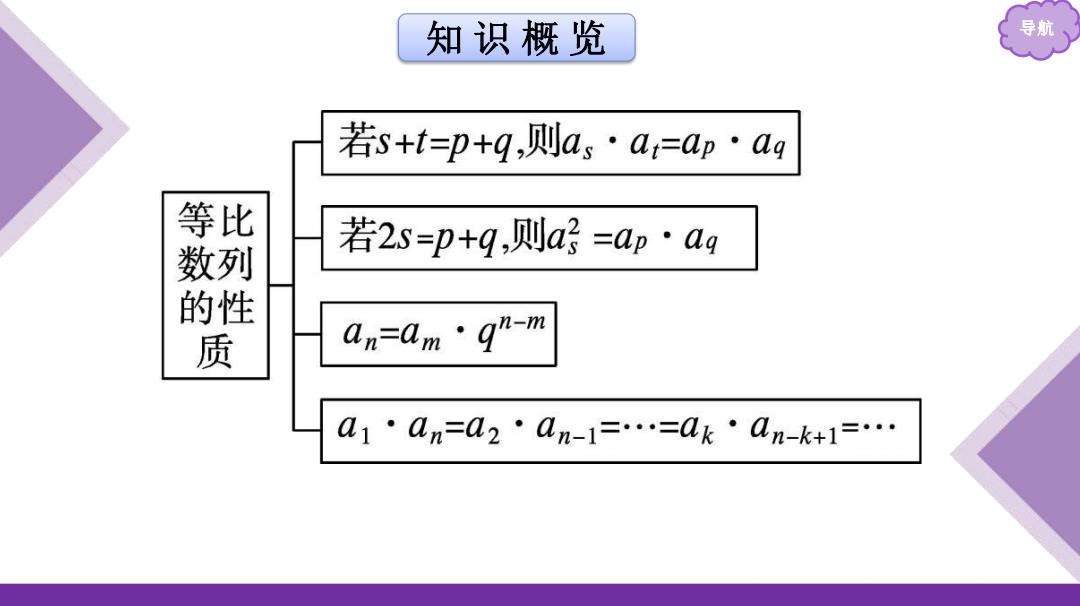
知识概览 导航 若s+t=p+q,则a,·a=ap·ag 等比 数 若2S=p+9,则a好=ap·ag 的性 质 an=am·q-m a1·an=02·an-1==0k·0n-k+1=…
知 识 概 览 导航

课前·基础认知 等比数列的性质 1.一般地,已知{a是等比数列,若正整数5,tp,q满足s+p+q, 则a,,F 特别地,若2s=p+g,则a= 2.对有穷等比数列,与首末两项等距离”的两项之积等于首 末两项的 ,即a1am=2an-1=…=Lk0m-k+=…. 3.若数列{an,{bn均为等比数列,c为不等于0的常数,则数列 {car,a2,an-bn,{g也为
导航 等比数列的性质 1.一般地,已知{an }是等比数列,若正整数s,t,p,q满足s+t=p+q, 则asat = apaq . 特别地,若 2s=p+q,则𝒂𝒔 𝟐 = apaq . 2.对有穷等比数列,与首末两项“等距离”的两项之积等于首 末两项的 积 ,即a1·an=a2·an-1 =…=ak·an-k+1 =… . 3.若数列{an},{bn}均为等比数列,c 为不等于 0 的常数,则数列 {can},{𝒂𝒏 𝟐 },{an·bn}, 𝒂𝒏 𝒃𝒏 也为 等比数列 . 课前·基础认知