
全程设计 3.函数
3.函数

梳理·构建体系 归纳·核心突破
梳理·构建体系 归纳·核心突破
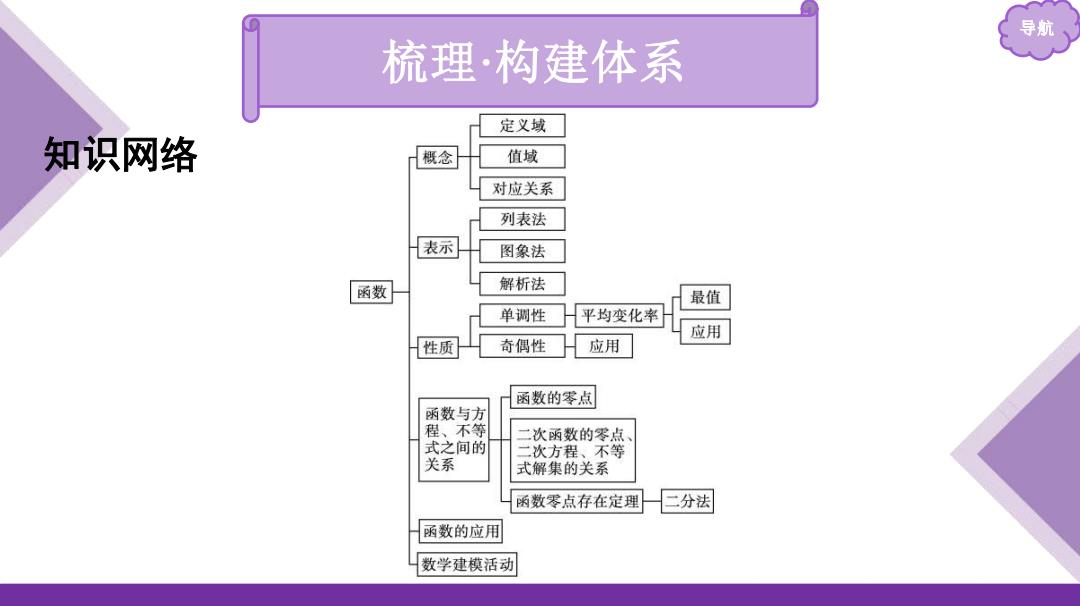
导航 梳理·构建体系 定义域 知识网络 概念 值域 对应关系 列表法 表示 图象法 函数 解析法 最值 单调性 平均变化率 应用 性质 奇偶性 应用 函数的零点 函数与方 程、不等 二次函数的零点 式之间的 二次方程、不等 关系 式解集的关系 函数零点存在定理 二分法 函数的应用 数学建模活动
导航 梳理 ·构建体系 知识网络

导航 要点梳理 1.什么是函数? 提示:一般地,给定两个非空实数集A与B,以及对应关系f如果 对于集合A中的每一个实数K,在集合B中都有唯一确定的实 数y与x对应,则称f为定义在集合A上的一个函数.记作y=x), x∈A,其中x称为自变量y称为因变量
导航 要点梳理 1.什么是函数? 提示:一般地,给定两个非空实数集A与B,以及对应关系f,如果 对于集合A中的每一个实数x,在集合B中都有唯一确定的实 数y与x对应,则称f为定义在集合A上的一个函数.记作y=f(x), x∈A,其中x称为自变量,y称为因变量

2.什么是函数的定义域、值域?什么是同一个函数? 提示:自变量取值的范围(即数集A)称为函数的定义域,所有函 数值组成的集合yly=f孔x),x∈A称为函数的值域, 如果两个函数表达式表示的函数定义域相同,对应关系也相 同(即对自变量的每一个值,两个函数表达式得到的函数值都 相等),则称这两个函数表达式表示的就是同一个函数, 3.函数有哪些表示方法? 提示:解析法、图象法、列表法
导航 2.什么是函数的定义域、值域?什么是同一个函数? 提示:自变量取值的范围(即数集A)称为函数的定义域,所有函 数值组成的集合{y|y=f(x),x∈A}称为函数的值域, 如果两个函数表达式表示的函数定义域相同,对应关系也相 同(即对自变量的每一个值,两个函数表达式得到的函数值都 相等),则称这两个函数表达式表示的就是同一个函数. 3.函数有哪些表示方法? 提示:解析法、图象法、列表法