
全程设计 章末核心素养整合
章末核心素养整合

知识体系构建 专题归纳突破
知识体系构建 专题归纳突破
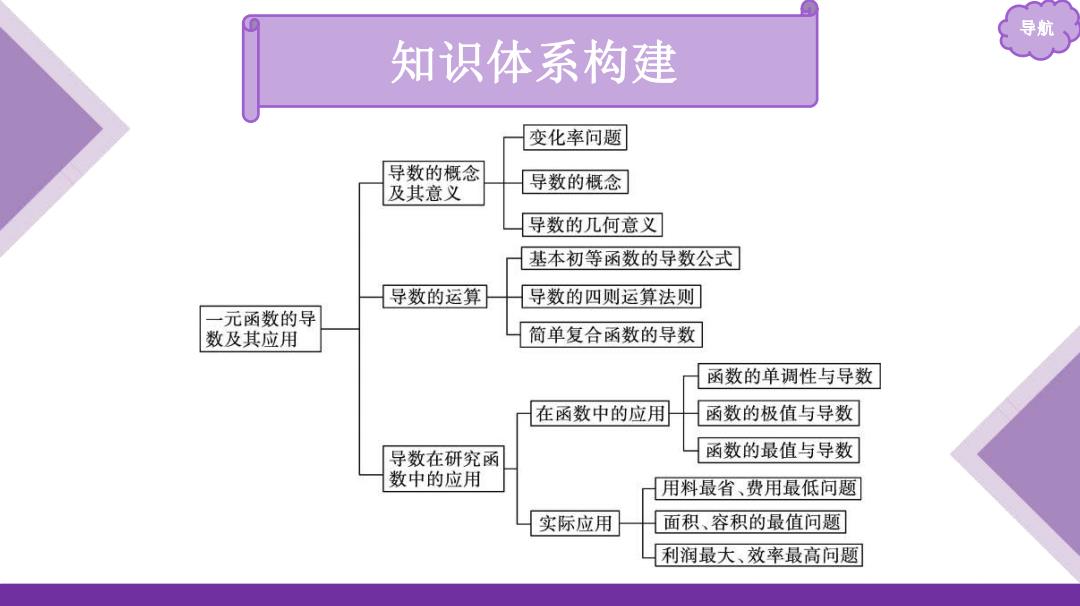
导航 知识体系构建 变化率问题 导数的概念 及其意义 导数的概念 导数的几何意义 基本初等函数的导数公式 导数的运算 导数的四则运算法则 一元函数的导 数及其应用 简单复合函数的导数 函数的单调性与导数 在函数中的应用 函数的极值与导数 导数在研究函 函数的最值与导数 数中的应用 用料最省、费用最低问题 实际应用 面积、容积的最值问题 利润最大、效率最高问题
导航 知识体系构建

导航 专题归纳突破 专题一导数的几何意义 利用导数的几何意义求切线方程时,关键是搞清所给的点是 不是切点
导航 专题一 导数的几何意义 利用导数的几何意义求切线方程时,关键是搞清所给的点是 不是切点. 专题归纳突破

导航 【典型例题1】已知函数fx)=c3+3x2-6c-11, g(c)=3x2+6x+12,直线y=c+9,且f'(-1)=0. (1)求的值; (2)是否存在实数k,使直线m既是曲线y=fx)的切线,又是曲 线y=gx)的切线?如果存在,求出k的值;如果不存在,说明理由
导航 【典型例题1】已知函数f(x)=ax3+3x 2 -6ax-11, g(x)=3x 2+6x+12,直线m:y=kx+9,且f'(-1)=0. (1)求a的值; (2)是否存在实数k,使直线m既是曲线y=f(x)的切线,又是曲 线y=g(x)的切线?如果存在,求出k的值;如果不存在,说明理由