
全程设计 第四章 数列 4.4* 数学归纳法
第四章 数列 4.4* 数学归纳法

素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 素养·目标定位 目标素养 1.通过实例,了解数学归纳法的原理,提升数学抽象素养. 2.能用数学归纳法证明一些简单的数学命题,提升逻辑推理素 养
导航 目 标 素 养 1.通过实例,了解数学归纳法的原理,提升数学抽象素养. 2.能用数学归纳法证明一些简单的数学命题,提升逻辑推理素 养. 素养·目标定位
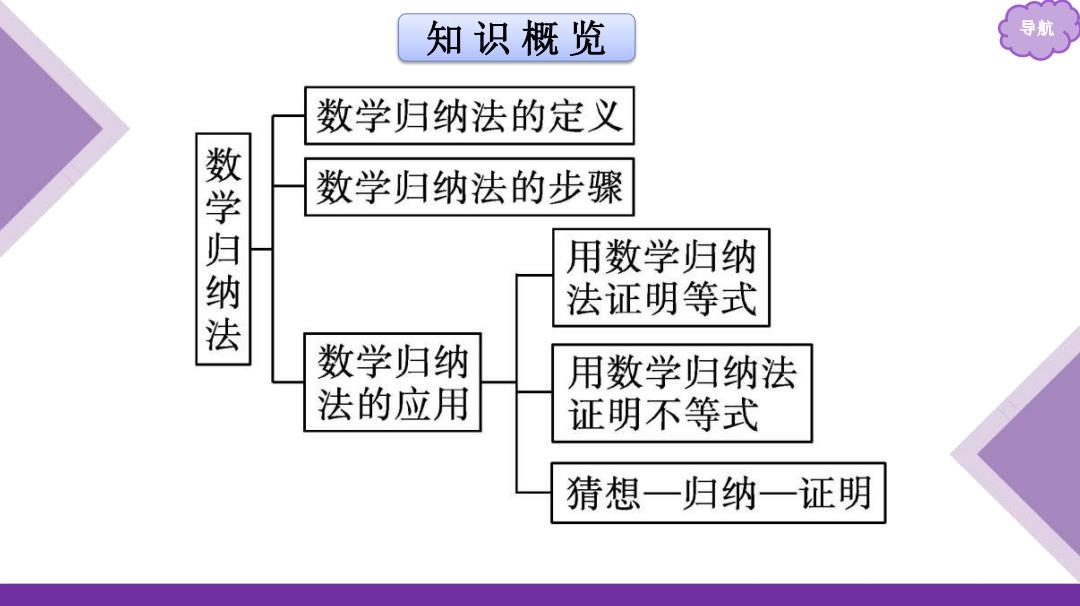
知识概览 导航 数学归纳法的定义 数学归纳 数学归纳法的步骤 用数学归纳 法证明等式 数学归纳 用数学归纳法 法的应用 证明不等式 猜想一归纳一证明
知 识 概 览 导航

导 课前·基础认知 1数学归纳法的定义 一 般地,证明一个与 n有关的命题,可按下列步骤 进行: (1)归纳奠基)证明当n=n(no∈N时命题成立; (2)归纳递推)以“当=k(k∈N*,k≥no)时命题成立”为条件, 推出“当 时命题也成立” 只要完成这两个步骤,就可以断定命题对从,开始的所有正 整数n都成立.这种证明方法称为数学归纳法
导航 1.数学归纳法的定义 一般地,证明一个与 正整数 n有关的命题,可按下列步骤 进行: (1)(归纳奠基)证明当n=n0 (n0∈N* )时命题成立; (2)(归纳递推)以“当n=k(k∈N* ,k≥n0 )时命题成立”为条件, 推出“当 n=k+1 时命题也成立” . 只要完成这两个步骤,就可以断定命题对从n0开始的所有正 整数n都成立.这种证明方法称为数学归纳法. 课前·基础认知