
特殊矢量场 有势场 A=grad u 4=-gradv rotA =0 u(x,y,2)= Px+∫+∫Rxyz)止 ·管形场 diA≡0 )d=-R(.y.)dy 4=rotB v=∫Pxy)d W=C(C为任何常数) ·调和场 div 0 xy)=-P(xy)-∫xy)d rot4=0 ex ux=∫-Q(xyk+∫P(xy)d lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn
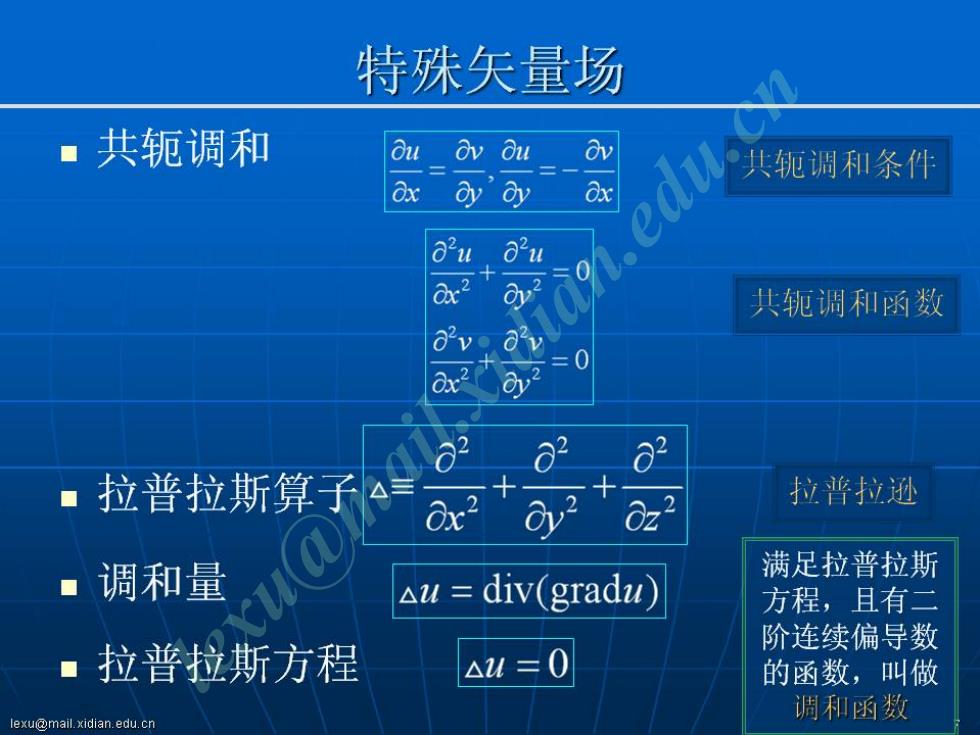
特殊矢量场 ·共轭调和 Ou Ov Ou edu. 轭调和条件 Cx? 共轭调和函数 O've 0'v =0 2 拉普拉斯算子 拉普拉逊 0z2 调和量 满足拉普拉斯 △u=div(gradu) 方程,且有二 阶连续偏导数 拉普拉斯方程 △2u=0 的函数,叫做 调和函数 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn
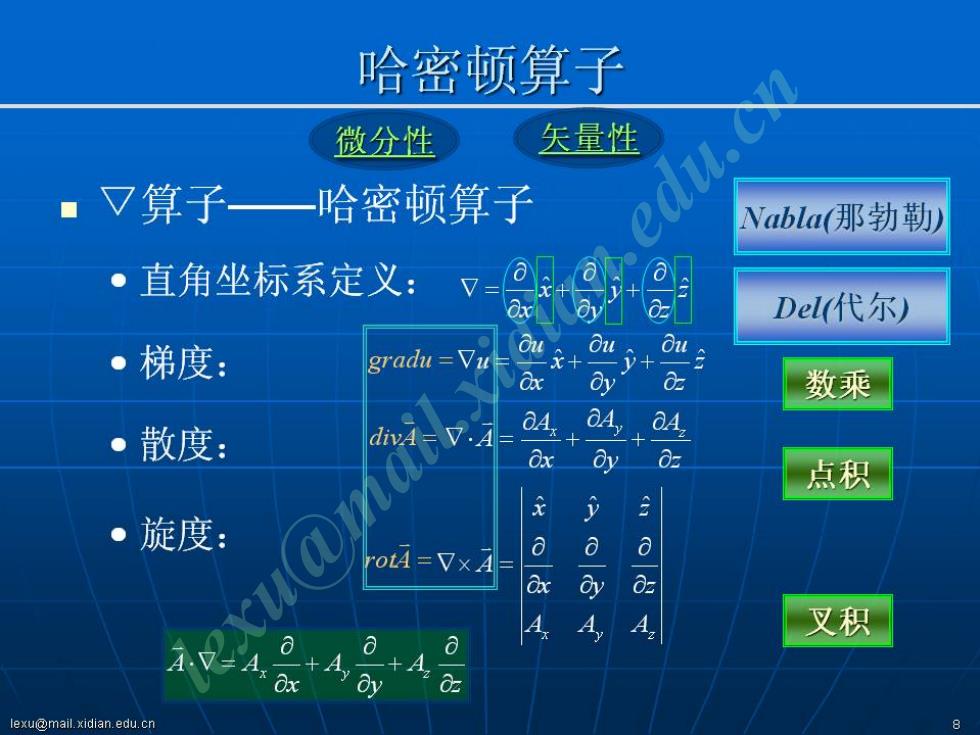
哈密顿算子 微分性 矢量性 。V算子一哈密顿算子 Nablat(那勃勒) 。直角坐标系定义:又 Del代尔) 。梯度: gradu Vu Ou V+ d 数乘 。散度: divA-V.A OA Ov 0 点积 ·旋度: A A 叉积 AV-4.7 Ay oy _tA: lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

哈密顿算子 。两个矢量恒等式 edu.Cx div(rot4)=0 V:(N×A④=0 旋无散 rot(gradu)=0 梯无旋 两个积分变换 线面 divAdv A.=vA 面→体 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn